
如图,用大小相同的小正方形拼大正方形,拼第1个大正方形需要4个小正方形,拼第2个大正方形需要9个小正方形,拼第3个大正方形需要16个小正方形,……,按照这样的拼法,第9个大正方形比第8个大正方形多______个小正方形.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第12章 全等三角形 单元测试 题型:解答题
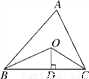
如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第12章 全等三角形 单元测试 题型:单选题
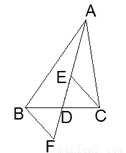
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】试题解析:∵AD是△ABC的中线, ∴BD=CD,又∠CDE=∠BDF,DE=DF, ∴△BDF≌△CDE,故④正确; 由△BDF≌△CDE,可知CE=BF,故①正确; ∵AD是△ABC的中线, ∴△ABD和△ACD等底等高, ∴△ABD和△ACD面积相等,故②正确; 由△BDF≌△CDE,可知∠FBD=∠ECD ∴BF∥CE,故③正确. 故选D.查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期七年级期末质量检测数学试卷 题型:解答题
如图,已知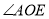 是平角,
是平角, 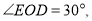
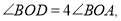 且OC平分
且OC平分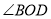 ,求
,求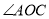 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期七年级期末质量检测数学试卷 题型:单选题
下列各数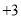 、
、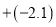 、
、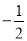 、0、
、0、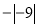 、
、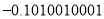 中,负有理数的个数是( )
中,负有理数的个数是( )
A. 2 B. 3 C. 4 D. 5
C 【解析】试题解析: 都是负有理数. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学 第二章 二次函数 单元检测卷 题型:填空题
已知二次函数y=﹣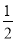 x2﹣2x+1,当x________时,y随x的增大而增大.
x2﹣2x+1,当x________时,y随x的增大而增大.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:解答题
“a2=0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,(x+2)2+1≥1,∴x2+4x+5≥1.试利用“配方法”解决下列问题:
(1)填空:因为x2﹣4x+6=(x )2+ ;所以当x= 时,代数式x2﹣4x+6有最 (填“大”或“小”)值,这个最值为 .
(2)比较代数式x2﹣1与2x﹣3的大小.
(1)﹣2;2;2;小;2;(2)x2﹣1>2x﹣3. 【解析】试题分析:(1)把原式利用平方法化为完全平方算与一个常数的和的形式,利用偶次方的非负性解答; (2)利用求差法和配方法解答即可. 试题解析:(1)x2-4x+6=(x-2)2+2, 所以当x=2时,代数式x2-4x+6有最小值,这个最值为2, 故答案为:-2;2;2;小;2; (2)x2-1-(2x...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com