
如果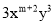 与
与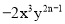 是同类项,则m、n的值分别是
是同类项,则m、n的值分别是
A. 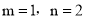 B.
B. 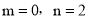 C.
C. 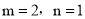 D.
D. 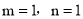
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:解答题
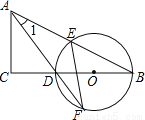
如图,在△ABC中,∠C= 90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1= ∠F;
(2)若CD= 3,EF=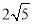 ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2017-2018学年七年级上学期期末考试数学试卷(WORD版) 题型:单选题
如果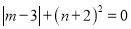 ,那么
,那么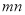 的值为( )
的值为( )
A. 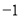 B.
B. 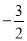 C. 6 D.
C. 6 D. 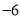
查看答案和解析>>
科目:初中数学 来源:内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
观察下列图形和所给表样中的数据后回答问题.
梯形个数 | 1 | 2 | 3 | 4 | 5 | …… |
图形周长 | 5 | 8 | 11 | 14 | 17 | …… |

当图形的周长为80时,梯形的个数为_________.
26 【解析】试题分析:仔细分析所给表格中的数据可得第一个图形的周长为,第二个图形的周长为,第三个图形的周长为,根据这个规律可得第n个图形的周长为,从而可以求得结果. 由题意得第n个图形的周长为, 当图形的周长为80时,,解得,即梯形的个数为26.查看答案和解析>>
科目:初中数学 来源:内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
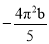 的系数是______ .
的系数是______ .
查看答案和解析>>
科目:初中数学 来源:内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列四个图中,能用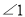 、
、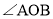 、
、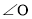 三种方法表示同一个角的是
三种方法表示同一个角的是
A. 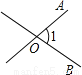 B.
B. 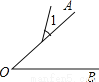 C.
C. 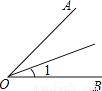 D.
D. 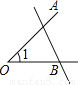
查看答案和解析>>
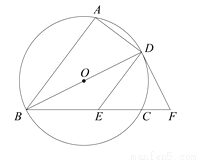
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF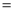 DE.
DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD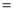 4,DE
4,DE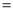 5,求DM的长.
5,求DM的长.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:单选题
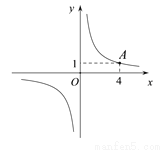
如图,反比例函数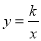 的图象经过点A(4,1),当
的图象经过点A(4,1),当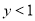 时,x的取值范围是( )
时,x的取值范围是( )
A. 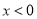 或
或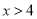 B.
B. 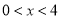 C.
C. 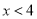 D.
D. 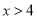
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
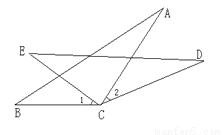
如图所示,CA=CD,∠1=∠2,BC=EC,求证:AB=DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com