
已知 中,
中, 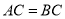 ,
, 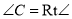 .如图,将
.如图,将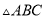 进行折叠,使点
进行折叠,使点 落在线段
落在线段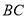 上(包括点
上(包括点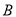 和点
和点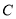 ),设点
),设点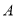 的落点为
的落点为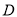 ,折痕为
,折痕为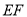 ,当
,当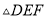 是等腰三角形时,点
是等腰三角形时,点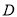 可能的位置共有( ).
可能的位置共有( ).

A. 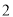 种 B.
种 B. 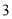 种 C.
种 C. 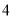 种 D.
种 D. 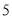 种
种
 综合自测系列答案
综合自测系列答案科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:单选题
如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )

A. 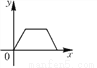 B.
B. 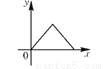 C.
C. 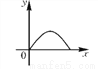 D.
D. 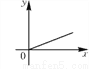
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:填空题
在实数范围内定义一种运算“﹡”,其规则为a﹡b=a2﹣b2,根据这个规则,求方程(x﹣2)﹡1=0的解为_____.
x1=1,x2=3 【解析】试题解析:∵﹡ ∴﹡1= 解方程 故答案为:查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
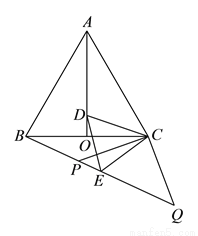
如图,等边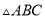 中,
中, 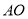 是
是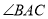 的角平分线,
的角平分线,  为
为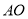 上一点,以
上一点,以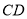 为一边且在
为一边且在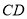 下方作等边
下方作等边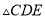 ,连接
,连接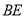 .
.
( )求证:
)求证: 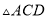 ≌
≌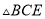 .
.
(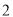 )延长
)延长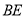 至
至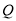 ,
, 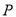 为
为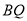 上一点,连接
上一点,连接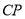 、
、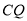 使
使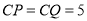 ,若
,若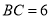 ,求
,求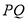 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:填空题
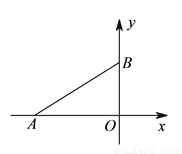
如图,在平面直角坐标系中, 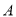 ,
, 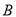 两点的坐标分别为
两点的坐标分别为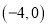 ,
, 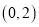 ,连接
,连接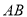 ,若以点
,若以点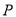 ,
, 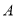 ,
, 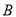 为顶点的三角形是等腰直角三角形,则点
为顶点的三角形是等腰直角三角形,则点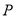 坐标为__________.
坐标为__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
不等式组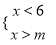 无解,
无解, 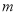 的取值范围是( ).
的取值范围是( ).
A. 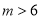 B.
B. 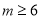 C.
C. 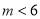 D.
D. 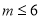
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
能不能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2.
能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2 【解析】试题分析:根据已知不等式的解集得出1﹣a<0, =2,求出方程的解即可. 试题解析:∵关于x的不等式(1﹣a)x>a﹣5的解集是x<2, ∴1﹣a<0, =2, 解得:a=, 经检验a=是方程=2的解, 即能找到这样的a值,使关于x的不等式(1﹣a)x>a﹣5的解集是x<2.查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
在函数y=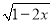 自变量x的取值范围是( )
自变量x的取值范围是( )
A. x≤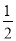 B. x<
B. x<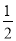 C. x≥
C. x≥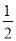 D. x>
D. x>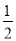
查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
如图:将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C1,D1处.若∠C1BA=50°,则∠ABE的度数为( )
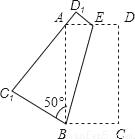
A. 15° B. 20° C. 25° D. 30°
B 【解析】根据折叠前后对应角相等可知. 【解析】 设∠ABE=x, 根据折叠前后角相等可知,∠C1BE=∠CBE=50°+x, 所以50°+x+x=90°, 解得x=20°. 故选B. “点睛”本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com