
如图,等边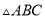 中,
中, 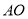 是
是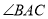 的角平分线,
的角平分线, 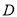 为
为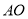 上一点,以
上一点,以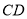 为一边且在
为一边且在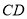 下方作等边
下方作等边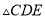 ,连接
,连接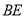 .
.
(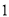 )求证:
)求证: 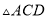 ≌
≌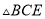 .
.
(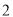 )延长
)延长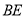 至
至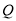 ,
, 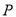 为
为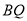 上一点,连接
上一点,连接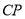 、
、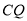 使
使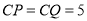 ,若
,若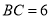 ,求
,求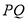 的长.
的长.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源:2018年春北师大版七年级数学下册活页测试卷:期末测试 题型:解答题
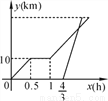
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
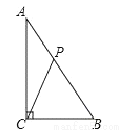
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
A. 5 B. 5或8 C. 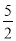 D. 4或
D. 4或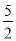
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:单选题
下列计算正确的是( )
A. a4+a2=a6 B. 2a•4a=8a C. a5÷a2=a3 D. (a2)3=a5
C 【解析】试题分析:A. a4+a2不是同类项,不能计算,故不正确; B.2a·4a=8a2,故不正确; C.根据同底数幂的除法,可知a5÷a2=a3,故正确; D.根据幂的乘方可知 (a3)3=a9,故不正确. 故选:C.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
解下列不等式(组).
(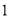 )
)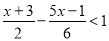 .
.
(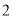 )
)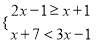 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:单选题
已知 中,
中, 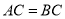 ,
, 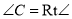 .如图,将
.如图,将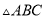 进行折叠,使点
进行折叠,使点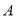 落在线段
落在线段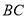 上(包括点
上(包括点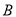 和点
和点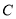 ),设点
),设点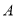 的落点为
的落点为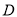 ,折痕为
,折痕为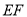 ,当
,当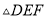 是等腰三角形时,点
是等腰三角形时,点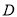 可能的位置共有( ).
可能的位置共有( ).

A. 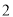 种 B.
种 B. 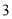 种 C.
种 C. 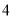 种 D.
种 D. 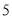 种
种
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
函数y=kx(k≠0)的图象过P(﹣3,3),则k=________ ,图象过________象限.
-1 二、四 【解析】根据题意,首先把P点坐标代入y=kx可得-3=3k,计算出k=-1,然后由k<0,再根据正比例函数的性质可得图象经过第二、四象限. 故答案为:﹣1;二、四.查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:解答题
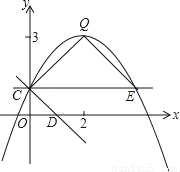
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com