
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点是(1,n),且与x的一个交点在点(3,0)和(4,0)之间,则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不等的实数根.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:安徽省2018年中考数学试卷 题型:单选题
如图,直线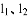 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为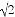 ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于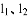 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )
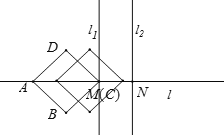
A. 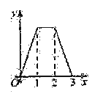 B.
B. 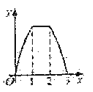 C.
C. 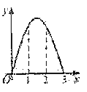 D.
D. 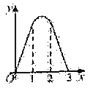
查看答案和解析>>
科目:初中数学 来源:华东师大版八年级下册 第19章 矩形、菱形与正方形 综合测试卷 题型:填空题
如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF=_______.
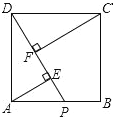
查看答案和解析>>
科目:初中数学 来源:浙教版九年级下册数学期末高效复习 专题1 二次函数(解析版) 题型:解答题
如图,在一面靠墙的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
(1)求S与x的函数关系式及自变量的取值范围;
(2)已知墙的最大可用长度为8 m,
①求所围成花圃的最大面积;
②若所围花圃的面积不小于20 m2,请直接写出x的取值范围.
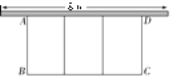
查看答案和解析>>
科目:初中数学 来源:浙教版九年级下册数学期末高效复习 专题1 二次函数(解析版) 题型:单选题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下说法不正确的是( )
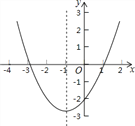
A. 根据图象可得该函数y有最小值
B. 当x=?2时,函数y的值小于0
C. 根据图象可得a>0,b<0
D. 当x<?1时,函数值y随着x的增大而减小
查看答案和解析>>
科目:初中数学 来源:浙教版九年级下册数学期末高效复习 专题1 二次函数(解析版) 题型:单选题
将抛物线y=2x2+4x-5的图象向左平移2个单位,再向上平移1个单位,所得抛物线表达式是( )
A. y=2(x+1)2-7 B. y=2(x+1)2-6
C. y=2(x+3)2-6 D. y=2(x-1)2-6
查看答案和解析>>
科目:初中数学 来源:江苏省常州市天宁分校2018届九年级第二次模拟考试数学试卷 题型:解答题
⑴ 阅读理解
问题1:已知a、b、c、d为正数, ,ac=bd,试说明a=d,b=c.
,ac=bd,试说明a=d,b=c.
我们通过构造几何模型解决代数问题. 注意到条件 ,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.

∵ac=bd,
∴AB·CD=BC·AD
∴
请你按照以上思路继续完成说明.
⑵ 深入探究
问题2:若a>0,b>0,试比较 和
和 的大小.
的大小.
为此我们构造图2所示的几何模型,其中AB为直径, O为圆心,点C在半圆上,CD⊥AB 于D,AD=a,BD=b.
请你利用图2所示的几何模型解决提出的问题2.
⑶ 拓展运用
对于函数y=x+ ,求当x>0时,求y的取值范围.
,求当x>0时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源:黑龙江省2017届九年级下学期期末考试数学试卷 题型:单选题
关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )
A. a≥1 B. a>1且a≠5 C. a≥1且a≠5 D. a≠5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com