
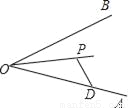
��ͼ����֪��PΪ��AOB�Ľ�ƽ�����ϵ�һ���㣬D������OA�ϵ�һ���㣬E��OB�ϵ�ijһ�㣬����PE=PD�����OEP���ODP��������ϵ��___________��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.1ͼ�ε���ת��2������ ���ͣ���ѡ��
��ͼ����ת�У�����˵��������ǣ�������
A. ͼ���ϵ�ÿһ�㵽��ת���ĵľ������ B. ͼ���ϵ�ÿһ��ת���ĽǶ���ͬ
C. ͼ���Ͽ��ܴ��ڲ����� D. ͼ����������������������Ӧ������������
A ��������Aѡ��,��ͼ����ת��,������ת������,ͼ���϶�Ӧ�㵽��ת���ĵľ������,��Aѡ�����, Bѡ��,ͼ���ϵ�ÿһ��ת���ĽǶȶ�������ת��,��Bѡ����ȷ, Cѡ��,ͼ����һ��Ϊ��ת����,������㲻��, ��Cѡ����ȷ, Dѡ��,��תǰ������ͼ��ȫ��,��ͼ����������������������Ӧ������������, ��Dѡ����ȷ, ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������ʵĽ�һ����ʶ����Ԫ����4 ���ͣ���ѡ��
��һ�����������a������ɫ��������ȫ��ͬ������a�����к���ֻ��3����ÿ�ν��������Ⱥ���������һ���������ɫ�ٷŻذ��䣮ͨ�������ظ�����ʵ����֣����������Ƶ���ȶ���25%����ô���������a��Լ�ǣ� ����
A. 12 B. 9 C. 4 D. 3
A �����������������Ƶ���ȶ���25%����=25%�����ɼ����a��ֵ �������� �����������Ƶ���ȶ���25%����=25%����ã�a=12�� �ʱ���ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�2������ ���ͣ������
��������y=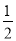 x2����״�Ϳ��ڷ�����ͬ������Ϊ��3��1���Ķ��κ�������ʽΪ______��
x2����״�Ϳ��ڷ�����ͬ������Ϊ��3��1���Ķ��κ�������ʽΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�2������ ���ͣ���ѡ��
������y=ax2+bx+c�����㣨3��0���ͣ�2����3��������ֱ��x=1Ϊ�Գ��ᣬ�����Ľ���ʽΪ��������
A. y=��x2��2x��3 B. y=x2��2x��3 C. y=x2��2x+3 D. y=��x2+2x��3
B ���������������������֪����������������߽���ʽ�����ɶԳ��ṫʽ�г���ϵʽ���������a��b��c��ֵ������ȷ��������ʽ�� �������� ��(3,0)��(2,?3)���������߽���ʽ�ã� �� ��ֱ��x=1Ϊ�Գ���,�õ�=1����b=?2a�� ���뷽����ã� �� ��ã�a=1��b=?2��c=?3�� �������߽���ʽΪy=x2?2x?3�� ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� ȫ���������ж� �������ϰ�����𰸣� ���ͣ������
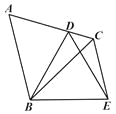
��ͼ����ABC�ǵȱ������Σ���DΪ AC����һ�㣬��BDΪ�����ȱߡ�BDE�� ����CE����CD��1��CE��3����BC��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� ȫ���������ж� �������ϰ�����𰸣� ���ͣ������
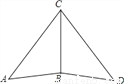
��ͼ����֪��ABC�ա�DBC����A=45�㣬��ACD=76�㣬���DBC�Ķ���Ϊ_________�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� ȫ���������ж� �������ϰ�����𰸣� ���ͣ������
��ͼ��ʾ�� AB=AC��AD=AE����BAC=��DAE����1=25�㣬��2=30�㣬���3=_____.
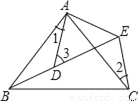
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ��棨2012�� ���꼶�ϲ�ͬ����ϰ��1.2���ε����� ���ͣ������
MΪ����ABCD��BC��һ�㣬DN��AM��N��AB=3��BC=7��AM=5����DN=______��
�����������ı���ABCD�Ǿ��Σ���AD=BC=7����B=90�㣬AD//BC�� ���AMB=��DAN�� �ߡ�AND=90��=��B�� ���ADN�ס�MAB�� �࣬�� ����DN= �� �ʴ�Ϊ�� .�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com