
��ͼ��AB�ǡ�O��ֱ������C��D��Բ�ϣ����ı���AOCD��ƽ���ı��Σ�����D����O�����ߣ��ֱ�OA���ӳ�����OC���ӳ����ڵ�E��F������BF.
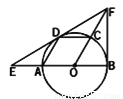
��1����֤��BF�ǡ�O�����ߣ�
��2����֪Բ�İ뾶Ϊ1����EF�ij�.
��1��֤������������2��EF=2. �����������������(1)����֤���ı���AOCD�����Σ��Ӷ��õ���AOD=��COD=60�㣬�ٸ������ߵ����ʵá�FDO=90�㣬����֤����FDO�ա�FBO�õ���ODF=��OBF=90�㣬Ȼ��������ߵ��ж��������ɵõ����ۣ�(2)����Rt��OBF�У�����60�ȵ����еĶ�����⣮ ���������(1)������OD����ͼ�����ı���AOCD��ƽ���ı��Σ���OA=OC... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰����꼶��ѧ�²���ϰ���ھ��´����� ���ͣ������
������ʽ��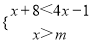 �Ľ⼯��x��3����m��ȡֵ��Χ��________��
�Ľ⼯��x��3����m��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�����ĸ����У��������ǣ�������
A. ����+2�� B. ��|��1| C. ����1��2 D. 0
C ���������ߩ���+2��=��2����|��1|=��1������1��2=1�� �ࣨ��1��2��0����|��1|������+2���� ���������ǣ���1��2����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ��AC=AD��BC=BD�����ABC�ա�______��Ӧ�õ��ж������ǣ���д��______��
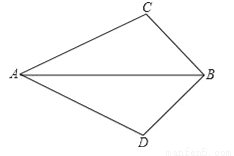
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡƽ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�����������У��١�A+��B=��C���ڡ�A����B����C=1�� 2��3���ۡ�A=90�㩁��B���ܡ�A=��B=��C�У���ȷ����ABC��ֱ�������ε������У� ������
A. 1�� B. 2�� C. 3�� D. 4��
C ������������Ϊ��A+��B=��C,��2��C=180��,��C=90�㣬���ԡ�ABC��ֱ�������Σ� ����Ϊ��A:��B:��C=1:2:3,���A=x,��x+2x+3x=180,x=30��,��C=30���3=90�㣬���ԡ�ABC��ֱ�������Σ� ����Ϊ��A=90��?��B,���ԡ�A+��B=90��,���C=180��?90��=90�㣬���ԡ�ABC��ֱ�������Σ� ����Ϊ3��A=2��B=��C...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��24�� Բ ��Ԫ���Ծ� ���ͣ������
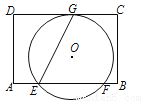
��ͼ���ھ���ABCD�У�AD��8��E�DZ�AB��һ�㣬��AE�� AB����O������E�����CD����ֱ�������ڵ�G����GEBΪ��ǣ������AB����ֱ�߽�����һ��F����EG��EF��
AB����O������E�����CD����ֱ�������ڵ�G����GEBΪ��ǣ������AB����ֱ�߽�����һ��F����EG��EF��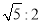 ������AD��BC���ڵ�ֱ�����O����ʱ��AB�ij��� .
������AD��BC���ڵ�ֱ�����O����ʱ��AB�ij��� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��24�� Բ ��Ԫ���Ծ� ���ͣ������
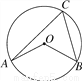
��ͼ��OA��OB�ǡ�O�İ뾶����C�ڡ�O�ϣ�����AC��BC������AOB��120�㣬���ACB�� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��3�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ������
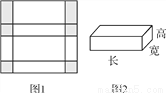
ͼ1�DZ߳�Ϊ30 cm��������ֽ�壬�õ���Ӱ�����۵���ͼ2��ʾ�ij�������ӣ���֪�ó�����Ŀ��Ǹߵ�2���������������_____________cm3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��23�� ��ת ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ����ABC�Ƶ�C��˳ʱ����ת15�㵽��DEC������Aǡ����DE�ϣ����BAE�Ķ���Ϊ��������
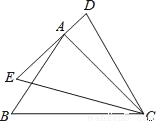
A. 15�� B. 55�� C. 65�� D. 75��
A ������������������ߡ�ABC�Ƶ�C��˳ʱ����ת15�㵽��DEC�� ���ACD=15�㣬��BAC=��D�� �ߡ�EAC=��D+��ACD�� ����BAE+��BAC=��D+��ACD�� ���BAE=��ACD=15�㣮 ��ѡA���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com