
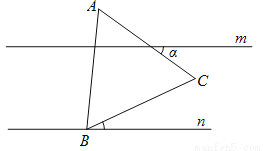
如图所示, 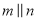 ,等边三角形
,等边三角形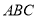 的顶点
的顶点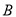 在直线
在直线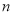 上,边
上,边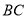 与直线
与直线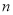 所夹的锐角为
所夹的锐角为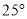 ,则
,则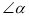 的度数为( )
的度数为( )
A. 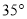 B.
B. 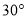 C.
C. 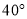 D.
D. 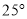
科目:初中数学 来源:黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积= 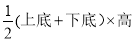 ).
).
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
数轴上表示一个数的点与原点的距离是6,那么这个数是_______.
±6 【解析】【解析】 ∵|±6|=6,∴数轴上表示一个数的点与原点的距离是6,那么这个数是±6.故答案为:±6.查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:填空题
如图,在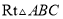 中,
中, 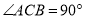 ,
, 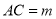 ,
, 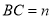 ,分别以三角形的三条边为边作正方形.
,分别以三角形的三条边为边作正方形.
( )若三个正方形的位置如图
)若三个正方形的位置如图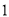 所示,其中阴影部分的面积
所示,其中阴影部分的面积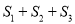 的值为__________.(结果用含
的值为__________.(结果用含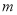 ,
, 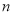 的代数式表示)
的代数式表示)
(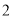 )若三个正方形的位置如图
)若三个正方形的位置如图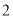 所示,其中阴影部分的面积
所示,其中阴影部分的面积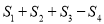 的值为__________.(结果用含
的值为__________.(结果用含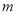 ,
, 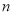 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:单选题
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
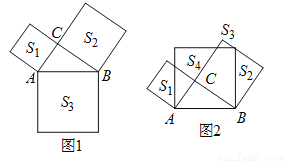
如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速倒入乙容器中. 图2中,线段AB、线段CD分别表示容器中的水的深度h(厘米)与倒入时间t(分钟)的函数图像.
(1)请说出点C的纵坐标的实际意义;
(2)经过多长时间,甲、乙两个容器中的水的深度相等?
(3)如果甲容器的底面积为10cm2,求乙容器的底面积.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
(1)计算: 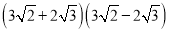 ; (2)解方程:
; (2)解方程: 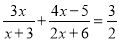 .
.
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:解答题
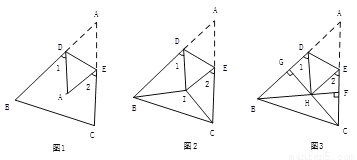
探究(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A的关系?直接写出结论,不必说明理由.
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数;
应用(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:单选题
如图,折叠直角三角形纸片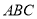 ,使两锐角顶点
,使两锐角顶点 重合,设折痕为
重合,设折痕为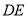 .若
.若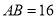 ,
, 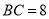 ,则
,则 的长是( )
的长是( )

A. 6 B. 8 C. 10 D. 12
A 【解析】设BD= ,则AD=AB-BD= , 由折叠的性质可得:DC=AD= , ∵在Rt△BCD中,DC2=BD2+BC2, ∴,解得: ,即BD=6. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com