
将函数y=x2的图象向右平移2个单位得函数y1的图象,将y与y1合起来构成新图象,直线y=m被新图象依次截得三段的长相等,则m=___________
【解析】试题解析:∵二次函数y=x2的图象向右平移2个单位, ∴平移后的解析式为:y=(x-2)2, 把y=m代入y=x2得m=x2,解得x=±, 把y=m代入y=(x-2)2得m=(x-2)2,解得x=2±, 当0<m<1时,则-(-)=2--,解得m=, 当m>1时,则2+-=-(2-),解得m=4, 故答案为或4.科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:填空题
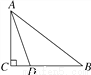
如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
把二次函数y=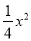 +x﹣1化为y=a(x﹣h)2+k的形式是( )
+x﹣1化为y=a(x﹣h)2+k的形式是( )
A. y=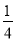 (x+1)2+2 B. y=
(x+1)2+2 B. y=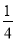 (x+1)2﹣2 C. y=
(x+1)2﹣2 C. y=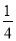 (x﹣2)2+2 D. y=
(x﹣2)2+2 D. y=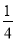 (x+2)2﹣2
(x+2)2﹣2
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
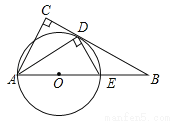
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=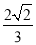 ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
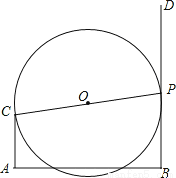
如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
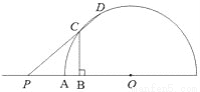
如图,半圆O的半径OA=4,P是OA延长线上一点,线段OP的垂直平分线分别交OP、半圆O于B、C两点,射线PC交半圆O于点D.设PA=x,CD=y,则能表示y与x的函数关系的图象是( )
A.  B.
B. 
C.  D.
D. 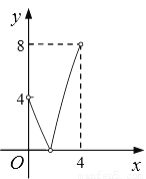
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A. 点P在⊙O上 B. 点P在⊙O内 C. 点P在⊙O外 D. 无法确定
C 【解析】试题解析:∵⊙O的半径为5,点P到圆心O的距离为6, ∴点P到圆心O的距离大于圆的半径, ∴点P在⊙O外. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
能判定四边形ABCD为平行四边形的是( ).
A. AB∥CD,AD=BC
B. ∠A=∠B,∠C=∠D
C. AB=CD,AD=BC
D. AB=AD,CB=CD
C 【解析】选项C中,两组对边分别相等的四边形是平行四边形.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第6章实数单元检测卷 题型:解答题
计算: 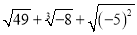 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com