练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知y与x+2成反比例，当x=4时，y=2，当x=0时，y=_____．

    6 【解析】∵y与x+2成反比例， ∴设y= （k≠0）， ∵x=4时，y=2， ∴=2， 解得k=12， ∴y= ， ∴当x=0时，y==6， 故答案为：6．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

    已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为（　　）

    A. ﹣3 B. 3 C. ﹣1 D. 1

    A 【解析】【解析】 ∵点A（1，a）、点B（b，2）关于原点对称，∴b=﹣1，a=﹣2，a+b=﹣3，故选A．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：填空题

    已知关于x的二次函数y=ax2+（a2﹣1）x﹣a的图象与x轴的一个交点的坐标为（m，0），若3＜m＜4，则a的取值范围是_____．

    ＜a＜或﹣4＜a＜﹣3 【解析】∵y=ax2+（a2﹣1）x﹣a=（ax﹣1）（x+a）， ∴当y=0时，可解得：x1=，x2=﹣a， ∴抛物线与x轴的交点为（，0）和（﹣a，0）． ∵抛物线与x轴的一个交点的坐标为（m，0）且2＜m＜3， ∴（1）当a＞0时，3＜＜4，解得； （2）当a＜0时，3＜﹣a＜4，解得﹣4＜a＜﹣3． 综上所述，a的取值范围是...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：解答题

    已知抛物线y=ax2+bx+c 如图所示，直线x=-1是其对称轴，

    （1）确定a，b，c， Δ=b2-4ac的符号，

    （2）求证：a-b+c>0，

    （3）当x取何值时，y>0；当x取何值时y<0.

    （1）a<0，b<0，c>0，b2-4ac>0； （2）a-b+c>0； （3）当-30 ，∴当x<-3或x>1时，y<0. 【解析】 思路点拨：（1）根据开口方向确定a的符号，根据对称轴的位置确定b的符号，根据抛物线与y轴的交点确定c的符号，根据抛物线与x轴交点的个数确定b2-4ac的符号； （2）根据图象和x=-1的函数值确定a-b+c与0的关系； ...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：填空题

    一个两位数，个位数字比十位数字大3，个位数字的平方刚好等于这个两位数，则这个两位数是________．

    25或36 【解析】试题分析：设十位数字为x则个位数字为x+3,所以两位数为10x+x+3 = 11x+3，因为个位数字的平方刚好等于这个两位数，所以= 11x+3，解得x= 2或3,所以得到25,或36．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：单选题

    如图，将三角尺ABC（其中∠ABC＝60°，∠C＝90°）绕B点按顺时针方向转动一个角度到A1BC1的位置，使得点A，B，C1在同一条直线上，那么这个角度等于（ ）．

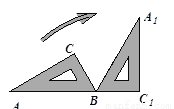
    A. 120° B. 90° C. 60° D. 30°

    A 【解析】试题分析：根据旋转图形的性质可得：旋转的角度为180°-60°=120°.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：单选题

    下列方程中，一元二次方程是（　　）

    A. 2x2﹣3xy+4=0 B. 2x2﹣（x+1）2=2+x2

    C. 3x2+x=20 D. ax2+bx+c=0

    C 【解析】A、该方程中含有2个未知数，不是一元二次方程，故本选项错误；B、由原方程得到： 2x+3=0，不含有二次项，不是一元二次方程，故本选项错误；C、该方程符合一元二次方程的定义，故本选项正确；D、当a=0时，它不是一元二次方程，故本选项错误， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    一次函数 y=ax+b，若 a+b=1，则它的图象必经过点（ ）

    A. (-1,-1) B. (-1, 1) C. (1, -1) D. (1, 1)

    D 【解析】试题解析: 一次函数y=ax+b只有当x=1，y=1时才会出现a+b=1， ∴它的图象必经过点（1，1）． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：解答题

    如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，…，∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An．设∠A=θ．则：

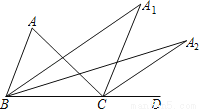
    （1）求∠A1的度数；

    （2）∠An的度数．

    （1）∠A1=；（2）∠An= 【解析】（1）∵BA1是∠ABC的平分线，CA1是∠ACD的平分线， ∴∠A1BC=∠ABC，∠A1CD=∠ACD， 又∵∠ACD=∠A+∠ABC，∠A1CD=∠A1BC+∠A1， ∴（∠A+∠ABC）=∠ABC+∠A1， ∴∠A1=∠A， ∵∠A=θ， ∴∠A1=； （2）同理可得∠A2=∠A1=•=， 所以∠...

    查看答案和解析>>

    同步练习册答案