
圆内接正六边形的边心距为2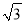 ,则这个正六边形的面积为_____cm2.
,则这个正六边形的面积为_____cm2.
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
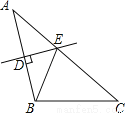
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为 .
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
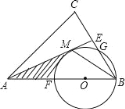
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:单选题
把抛物线y=﹣x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. y=﹣(x﹣1)2﹣3 B. y=﹣(x+1)2﹣3
C. y=﹣(x﹣1)2+3 D. y=﹣(x+1)2+3
C 【解析】试题解析:根据二次函数的图象平移规律可知: 把抛物线向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为: 故选C.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
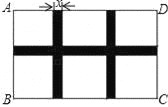
A. (40﹣x)(26﹣2x)=144×6
B. (40﹣2x)(26﹣x)=144×6
C. (40﹣2x)(26﹣x)=144÷6
D. (40﹣x)(26﹣2x)=144÷6
B 【解析】试题分析:设通道的宽度为x(m), 根据题意得(40﹣2x)(26﹣x)=144×6, 故选B.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
一元二次方程x2﹣3x+2=0 的两根分别是x1、x2,则x1+x2的值是( )
A. 3 B. 2 C. ﹣3 D. ﹣2
A 【解析】试题分析:这里a=1,b=﹣3, 则x1+x2=﹣=3, 故选A.查看答案和解析>>
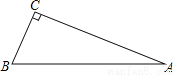
科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:单选题
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
A. 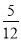 B.
B. 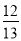 C.
C. 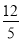 D.
D. 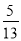
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为( ,
, 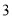 ),(
),(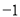 ,
, 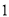 ).
).
(1)请在如图所示的网格平面内,作出平面直角坐标系;
(2)请作出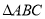 关于
关于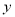 轴对称的
轴对称的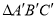 ;
;
(3)写出点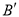 的坐标为___ __;
的坐标为___ __;
(4)△ABC的面积为__ _ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com