
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
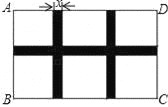
A. (40﹣x)(26﹣2x)=144×6
B. (40﹣2x)(26﹣x)=144×6
C. (40﹣2x)(26﹣x)=144÷6
D. (40﹣x)(26﹣2x)=144÷6
B 【解析】试题分析:设通道的宽度为x(m), 根据题意得(40﹣2x)(26﹣x)=144×6, 故选B. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
在一组数据中,随机抽取50个作为样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.12,那么这个样本中的数据落在54.5~57.5之间的有__个.
6 【解析】50×0.12=6(个).查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:填空题
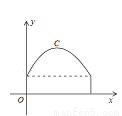
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米,该抛物线的函数表达式为 ______ .
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:解答题
某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)某日,宾馆了解当天的住宿情况,得到以下信息:
①当日所获利润不低于5000元,
②宾馆为游客居住的房间共支出费用没有超过600元,
③每个房间刚好住满2人.
问:这天宾馆入住的游客人数最少有多少人?
(1)y=50-x,(0≤x≤50,且x为整数);(2)每间房价定价为320元时,宾馆每天所获利润最大,最大利润是9000元;(3)20人 【解析】试题分析:(1)根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题. (2)构建二次函数,利用二次函数的性质解决问题. (3)根据条件列出不等式组即可解决问题. 试题解析:(1)根据题意,得:y=50﹣x,(0≤x≤5...查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:填空题
圆内接正六边形的边心距为2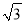 ,则这个正六边形的面积为_____cm2.
,则这个正六边形的面积为_____cm2.
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
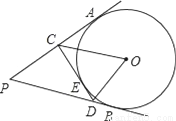
A. 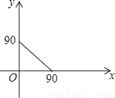 B.
B. 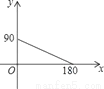
C. 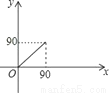 D.
D. 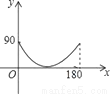
查看答案和解析>>
科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:解答题
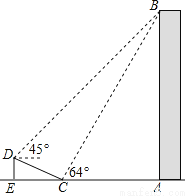
如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: 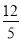 ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:单选题
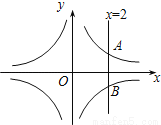
如图,直线x=2与反比例函数y=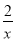 、y=
、y=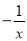 的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( )
的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( )
A. 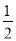 B. 1 C.
B. 1 C. 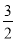 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x>ax+4的解集为 .
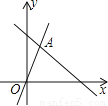
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com