
已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过点(-1,0)且平行于y轴的直线.
(1)求m,n的值;
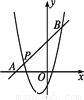
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.
(1)m=2,n=-2;(2)一次函数的表达式为y=x+4. 【解析】试题分析:(1)利用对称轴公式求得,把代入二次函数进而就可求得; (2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得的纵坐标,代入二次函数的解析式中求得的坐标,然后利用待定系数法就可求得一次函数的表达式. 试题解析:(1)由题意得解得 (2)如图,分别过点P,B作x轴的垂线,垂...科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:单选题
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:解答题
某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 | 优惠办法 |
少于300元 | 不预优惠 |
低于600元但不低于300元 | 九折优惠 |
600元或超过600元 | 其中600元部分给予九折优惠,超过600元部分给予八折优惠 |
(1)王老师一次性购物600元,他实际付款_________元.
(2)若顾客在该超市一次性购物x元,当x小于600元但不小于300时,他实际付款_____________元,当x大于或等于600元时,他实际付款______________元.(用含x的代数式表示).
(3)如果王老师两次购物货款合计920元,第一次购物的货款为a元(200<a<300),用含a 的代数式表示两次购物王老师实际付款多少元.
(1)540;(2)0.9x,(0.8x+60);(3)两次购物王老师实际付款(0.2a+796)元. 【解析】试题分析:(1)600元按9折付款,计算即可得; (2)当x小于600元但不小于300时,按9折付款,即为0.9x元; 当x大于或等于600元时,前600元按9折付款,超过部分按8折付款,即:0.9×600+0.8(x-600),整理即可得; (3)王老师第一次购...查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:单选题
有理数a,b在数轴上的位置如图所示,则化简|b-a|+a的结果为( )
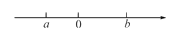
A. b B. -b C. -2a-b D. 2a-b
A 【解析】观察数轴可得:a<0查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:单选题
 的相反数是( )
的相反数是( )
A. 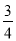 B.
B. 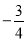 C.
C. 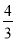 D.
D. 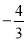
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:填空题
已知二次函数y=ax2-bx+c的图象经过点(-1,0),且a,b,c均为非零实数,则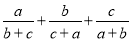 的值是_____.
的值是_____.
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:单选题
已知函数y=x2-2x-2的图象如图,根据其中提供的信息,可求得使y≥1成立的x的取值范围是 ( )
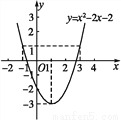
A. -1≤x≤3 B. -3≤x≤1 C. x≥-3 D. x≤-1或x≥3
D 【解析】试题分析:根据二次函数的图像可知:当x≤-1或x≥3时,y≥1,故选:D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:填空题
关于x、y的二元一次方程组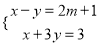 的解满足x +y>0,则m的取值范围是_____.
的解满足x +y>0,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:甘肃省平凉市崆峒区2017-2018学年度第一学期期末数学试卷及答案 题型:解答题
某学校校长寒假将带领该校市级三好学生去旅游。甲旅行社说:“若校长买全票一张,则其学生可享受半价优惠。”乙旅行社说:“包括校长在内全部按全票的6折优惠”。若全票价为240元,则:
(1)设学生数为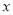 ,分别计算两家旅行社的收费(用含
,分别计算两家旅行社的收费(用含 的式子表示);
的式子表示);
(2)如何选择两家旅行社,可使学校更划算。
详见解析. 【解析】试题分析:(1)首先理解题意,根据题意即可求得y甲,y乙与x的关系式,注意化简; (2)分别从当y甲=y乙时,当y甲>y乙时,当y甲<y乙时去分析,通过解一元一次方程与不等式,即可求得答案. 试题解析:【解析】 (1)根据题意得: y甲=240+50%×240x=120x+240,y乙=240×60%(x+1)=144x+144; (2)当y甲=...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com