练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知4<m<5,则关于x的不等式组的整数解共有( 　)

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】解不等式组得： ， 又 4
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型：解答题

    因式分【解析】

    原式= 【解析】原式= = =

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古呼伦贝尔市七年级（下）期中数学试卷 题型：单选题

    如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2017次运动后，动点P的坐标是（　　）

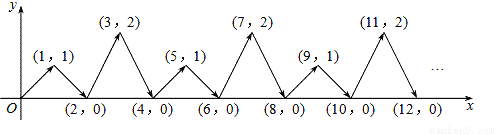
    A. （2017，0） B. （2017，1） C. （2017，2） D. （2016，0）

    B 【解析】经过第n次运动后，P的横坐标为n，纵坐标是以1，0，2，0四个数循环变化，2017÷4=504余1，所以P的纵坐标为1.经过第2017次运动后，P的坐标为（2017，1）. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期中测评 题型：解答题

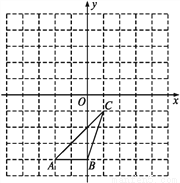
    如图所示的直角坐标系中,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).

    (1)在图中画出△ABC向左平移3个单位后的△A1B1C1;

    (2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2.

    （1）画图见解析；（2）画图见解析. 【解析】试题分析：（1）根据平移的方法找到A、B、C三点的对应点，然后顺次连接即可得； （2）根据旋转的方法找到A、B、C三点的对应点，然后顺次连接即可得. 试题解析：(1)如图所示,△A1B1C1为所求的三角形； (2)如图所示,△A2B2C2为所求的三角形.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期中测评 题型：填空题

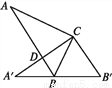
    如图,在Rt△ABC中,∠ACB=90°,∠ABC=58°,将Rt△ABC绕点C旋转到Rt△A'B'C',使点B恰好落在A'B'上,A'C交AB于点D,则∠ADC的度数为________.

    84° 【解析】由旋转的性质知：∠B′=∠ABC=58°，B′C =BC， 在等腰△BCB′中，由三角形内角和定理知： ∠BCB′=180°-2∠B′=64°， ∴∠BCD=90°-∠BCB′=26°， ∴∠ADC=∠ABC+∠BCD=58°+26°=84°， 故答案为：84°．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期中测评 题型：单选题

    如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC的大小是( 　)

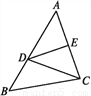
    A. 50° B. 100° C. 120° D. 130°

    B 【解析】∵DE垂直平分AC，∴DC=DA，∴∠ACD=∠A=50°， ∴∠BDC=∠A+∠ACD=100°， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型：解答题

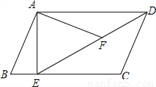
    如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

    （1）求证：△ADF∽△DEC；

    （2）若AB=4，AD=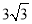，AE=3，求AF的长．

    （1）证明见解析；（2） 【解析】【试题分析】（1）因为∠AFE＝∠B，得 ,又因为∠ADF=∠CED，根据两角对应相等，两三角形相似. （2）在直角三角形ADE中，求出DE=6，再根据相似三角形对应边成比例，得=，即=解得AF=2； 【试题解析】 （1）∵∠AFE=∠B，∠AFE+∠AFD=180°，∠B+∠C=180°， ∴∠AFD=∠C， 又∵AD∥BC，...

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型：单选题

    在平面直角坐标系中，已知点O（0，0），A（2，4）.将线段OA沿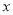 轴向左平移2个单位，记点O，A的对应点分别为点O1，A1，则点O1，A1的坐标分别是

    A. （0，0），（2，4） B. （0，0），（0，4）

    C. （2，0），（4，4） D. （－2，0），（0，4）

    D 【解析】试题解析：线段OA沿x轴向左平移2个单位，只须让原来的横坐标都减2，纵坐标不变即可． ∴新横坐标分别为0-2=-2，2-2=0，即新坐标为（-2，0），（0，4）．

    查看答案和解析>>

    科目：初中数学 来源：2018春季学北师大版九年级数学下册期中测评试卷 题型：解答题

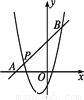
    已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过点(-1,0)且平行于y轴的直线.

    (1)求m,n的值;

    (2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.

    （1）m=2,n=-2；（2）一次函数的表达式为y=x+4. 【解析】试题分析：（1）利用对称轴公式求得，把代入二次函数进而就可求得； （2）根据（1）得出二次函数的解析式，根据已知条件，利用平行线分线段成比例定理求得的纵坐标，代入二次函数的解析式中求得的坐标，然后利用待定系数法就可求得一次函数的表达式． 试题解析：(1)由题意得解得 (2)如图,分别过点P,B作x轴的垂线,垂...

    查看答案和解析>>

    同步练习册答案