
探究证明:
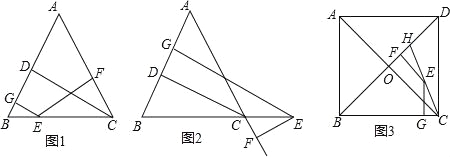
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型:填空题
数轴上表示1, 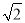 的点分别为A,B,且C、B两个不同的点到点A的距离相等,则点C所表示的数________.
的点分别为A,B,且C、B两个不同的点到点A的距离相等,则点C所表示的数________.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
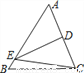
如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为( )
A. 16cm B. 18cm C. 26cm D. 28cm
B 【解析】因为:DE是△ABC中AC边的垂直平分线,所以:AD=BD, 则△DBC的周长=BD+CD+BC=AC+BC=18,故选B.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年八年级上学期第二次统测数学试卷 题型:填空题
a·a2=______ (x2)3÷x5=__________
x 【解析】a·a2=a1+2=a3;(x2)3÷x5=x6÷x5=x6-5=x, 故答案为:a3,x.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年八年级上学期第二次统测数学试卷 题型:单选题
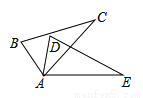
如图,△ABC≌△ADE,∠B=80°,∠C=30°,则∠EAD的度数为:
A. 70° B. 60° C. 50° D. 90°
B 【解析】试题解析:∵△ABC≌△ADE,∠B=80°,∠C=30°, ∴∠B=∠D=80°,∠E=∠C=30°, ∴∠EAD=180°-∠D-∠E=70°, 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
(本题8分)射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为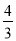 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
小张参加某公司招聘测试,他的笔试、面试、计算机操作得分分别为80分,85分,90分,若三项得分依次按照25%、20%、55%确定成绩,则小王的成绩是________.
86.5分 【解析】试题解析:2+3+5=10 根据题意得: 80×25%+85×20%+90×55% =20+17+49.5 =86.5(分) 答:小王的成绩是86.5分.查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:解答题
如图,已知△ABC:
(1)求作△ABC的内切圆⊙O,与边AB、BC、AC分别相切于点D、E、F;
(2)若AB=6,BC=8,AC=12,求AD、BE、CF的长度.

查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
抛物线y=2x2-12x+22 的顶点是( )
A. (3,-4) B. (-3,4) C. (3,4) D. (2,4)
C 【解析】∵, ∴抛物线的顶点坐标为(3,4). 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com