练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

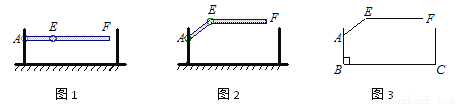
    某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC， EF∥BC，∠AEF=143°，AB=AE=1.3米，那么适合该地下车库的车辆限高标志牌为多少米？（结果精确到0.1．参考数据：sin 37° ≈ 0.60，cos 37° ≈ 0.80，tan 37° ≈ 0.75）

    适合该地下车库的车辆限高标志牌为2.1米 【解析】试题分析：过点E作EG⊥BC于点G，AH⊥EG于点H，则∠AHE=90°．先求出∠AEH=53°，则∠EAH=37°，然后在△EAH中，利用正弦函数的定义得出EH=AE•sin∠EAH，则栏杆EF段距离地面的高度为：AB+EH，代入数值计算即可． 试题解析：过点E作EG⊥BC于点G，AH⊥EG于点H． ∵EF∥BC， ∴∠G...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年八年级数学下册（人教版）：期末检测题(二) 题型：填空题

    一组数据2，3，x，5，7的平均数是5，则这组数据的中位数是_____．

    5 【解析】试题分析：根据平均数的定义可得：(2+3+x+5+7)÷5=5，解得：x=8，则这组数据为：2、3、5、7、8，即这组数据的中位数是5．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：解答题

    某种小商品的成本价为10元/kg，市场调查发现，该产品每天的销售量w（kg）与销售价x（元/kg）有如下关系w=﹣2x+100，设这种产品每天的销售利润为y（元）．

    （1）求y与x之间的函数关系式；

    （2）当售价定为多少元时，每天的销售利润最大？最大利润是多少？

    (1) y=-2+120x-1000;(2) 30元， 800元 【解析】试题分析： （1）由每天销售利润=每千克的盈利×每天的销售量，结合题意即可列出y与x间的函数关系式：y=(x-10)·w，再代入w=-2x+100化简即可得到所求函数关系式； （2）将（1）中所求函数关系式配方，即可得到所求答案. 试题解析： （1）由题意可得：y=w(x-10)=(-2x+10...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：单选题

    将抛物线y=x2-4x-4向左平移3个单位，再向上平移5个单位，得到抛物线的表达式为（ ）

    A. y=(x+1)2-13 B. y=(x-5)2-3 C. y=(x-5)2-13 D. y=(x+1)2-3

    A 【解析】先将一般式化为顶点式，根据左加右减，上加下减来平移 【解析】 将抛物线化为顶点式为： ，左平移3个单位，再向上平移5个单位 得到抛物线的表达式为 故选A． “点睛”本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型：解答题

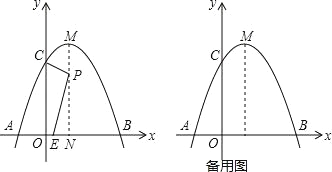
    如图，抛物线y=﹣x2+2x+3与x轴交于A、B两点，与y轴交于C点，对称轴与抛物线相交于点M，与x轴相交于点N．点P是线段MN上的一动点，过点P作PE⊥CP交x轴于点E．

    （1）直接写出抛物线的顶点M的坐标是 ．

    （2）当点E与点O（原点）重合时，求点P的坐标．

    （3）点P从M运动到N的过程中，求动点E的运动的路径长．

    （1）M（1，4）；（2）点P的坐标为：（1，）或（1，）；（3）E的运动的路径长为：． 【解析】 试题分析：（1）将解析式配成顶点式即可．（2）当点E与O重合时，设PN=m，过点C作CF⊥MN于F，由△ENP∽△PFC用相似比例建立方程解之即可．（3）找到左右两个极端位置即可．P在M点时，E在右边最运处，这个时候求出EN为对称轴右边的路径长度；E点在左侧时，设EN=y，PN=x，由△...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型：填空题

    古算趣题：“笨人执竿要进屋，无奈门框拦住竹，横多四尺竖多二，没法急得放声哭．有个邻居聪明者，教他斜竿对两角，笨伯依言试一试，不多不少刚抵足．借问竿长多少数，谁人算出我佩服．”若设竿长为x尺，则可列方程为_____．

    【解析】试题分析：设竿长为x尺，根据题意可得，则房门的宽为x﹣4，高为x﹣2，对角线长为x，然后根据勾股定理列出方程．（x﹣2）2+（x﹣4）2=x2．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型：填空题

    一元二次方程x2﹣2x+m=0总有实数根，则m应满足的条件是___________ ．

    m≤1 【解析】试题分析：∵方程x2﹣2x+m=0总有实数根，∴△≥0，即4﹣4m≥0，∴﹣4m≥﹣4，∴m≤1．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年福建省龙岩市上杭县城区片三校七年级（上）联考数学试卷 题型：解答题

    （1）将下列各数填在相应的集合里．

    ﹣（﹣2.5），（﹣1）2，﹣|﹣2|，﹣22，0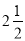， ，﹣1.5；

    正数集合{　 　 …}

    分数集合{　 　 …}

    （2）把表示上面各数的点画在数轴上，再按从小到大的顺序，用“＜“号把这些数连接起来．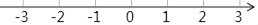

    (1) {﹣（﹣2.5），（﹣1）2， ，…}, {﹣（﹣2.5），，﹣1.5 …};（2）见解析 【解析】试题分析：（1）按有理数的分类标准进行分类即可； （2）先在数轴上表示各个数字，然后再进行比较即可. 试题解析：（1）正数集合{﹣（﹣2.5），（﹣1）2， …}； 分数集合{﹣（﹣2.5），，﹣1.5…}； （2）如图所示： 用“＜“号把这些数连接起来为...

    查看答案和解析>>

    科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：单选题

    如图，∠CAB＝∠DBA，再添加一个条件，不一定能判△ABC≌△BAD的是（ ）

    A. AC＝BD B. AD＝BC C. ∠DAB ＝∠CBA D. ∠C＝∠D

    B 【解析】试题分析：全等三角形的判定方法： ，A项符合，B项不能证明三角形全等，C项符合，D项符合．故选B．

    查看答案和解析>>

    同步练习册答案