
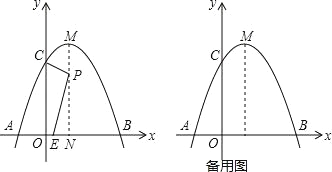
��ͼ��������y=��x2+2x+3��x�ύ��A��B���㣬��y�ύ��C�㣬�Գ������������ཻ�ڵ�M����x���ཻ�ڵ�N����P���߶�MN�ϵ�һ���㣬����P��PE��CP��x���ڵ�E��
��1��ֱ��д�������ߵĶ���M�������� ��
��2������E���O��ԭ�㣩�غ�ʱ�����P�����꣮
��3����P��M�˶���N�Ĺ����У���E���˶���·������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ�˽̰棩����ĩ�����(��) ���ͣ������
(1) 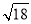 ��
��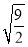 ��
��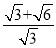 ��(
��(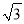 ��2)0��
��2)0��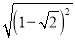 ��
��
(2)��֪x��2��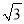 ��y��2��
��y��2��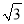 �������ʽ(
�������ʽ(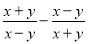 )��(
)��(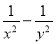 )��ֵ��
)��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ��ʦ��棩����ĩ���2 ���ͣ���ѡ��
��3x����3y�������в���ʽ��һ���������� �� ��
A. 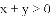
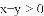
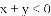
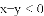
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��˳��2018����꼶��ѧ����ĩ��ѧ���������ѧ�Ծ� ���ͣ������
��һ��Բ�У����60���Բ�Ľ����Ի���Ϊ6��cm����ô���Բ���Եİ뾶Ϊ_____cm��
18�� �������������Բ�İ뾶Ϊcm����������ɵã� ����ã� (cm). �ʴ�Ϊ�� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��˳��2018����꼶��ѧ����ĩ��ѧ���������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����4��4�ķ����У�����16��С����ÿ��С�����DZ߳�Ϊ1�������Σ�O��A��B�ֱ���С�����εĶ��㣬������OAB�Ļ������ڣ�������
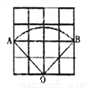
A. 2�� B. 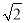 �� C. 2
�� C. 2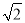 �� D.
�� D. 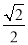 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
ij���³�����ڴ���װ�ˡ�����ʽ���ˡ�����ͼ1��ʾ����A������ת����֧�㣬��E���������ε�����㣮����������ʱ������AEF���ֻ��������ͼ2��ʾ��λ�ã���ʾ��ͼ��ͼ3��ʾ�����˿��Ⱥ��Բ��ƣ�������AB��BC�� EF��BC����AEF=143�㣬AB=AE=1.3�ף���ô�ʺϸõ��³���ij����߱�־��Ϊ�����ף��������ȷ��0.1���ο����ݣ�sin 37�� �� 0.60��cos 37�� �� 0.80��tan 37�� �� 0.75��
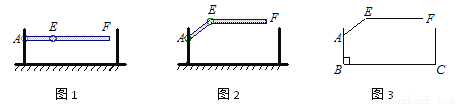
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����֪����ֽƬABCD�У�AB��1����ȥ������ABEF���õ��ľ���ECDF�����ABCD���ƣ���AD�ij�Ϊ_____��
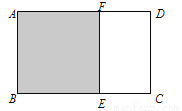
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�긣��ʡ�������Ϻ��س���Ƭ��У���꼶���ϣ�������ѧ�Ծ� ���ͣ������
10��С����ÿ��150ǧ��Ϊ��������ǧ������Ϊ�����������ǧ������Ϊ�������ֱ��Ϊ����6����3��0����3��+7��+3��+4����3����2��+1��
��1�����������Ƚϣ�10��С���ܼƳ����������ǧ�ˣ�
��2��10��С������һ������������ӽ���������
��3��ÿ��С���ƽ�������Ƕ���ǧ�ˣ�
��1������2ǧ�ˣ���2������������3��149.8ǧ��. �������������������1������-��6����3��0����3��+7��+3��+4����3����2��+1�ĺͣ��������������Ǹ��������㣻 ��2�����ݾ���ֵ���ɽ����жϣ�����ֵ��С�Ľӽ��������� ��3�����10��С����ÿ��150ǧ��Ϊʱ���������ټ��ϣ�1���еĽ����Ȼ������������10���������ÿ��С���ƽ�������� �����������1...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������ѧ2017-2018ѧ����꼶1���¿���ѧ�Ծ� ���ͣ������
���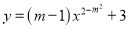 ��һ�κ�������
��һ�κ�������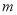 ��ֵ��________________.
��ֵ��________________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com