练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点A（－3，2）向左平移2个单位长度后得到的点的坐标为（ ）.

    A．（－3，0）  B．（－1，0）   C．（－1，2）   D．（－5，2）

    D 【解析】：∵点A（-3，2）向左平移2个单位长度， ∴新点的横坐标为-3-2=-5，纵坐标不变，即新点的坐标为（-5，2），故选D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版九年级下册数学第三章圆单元检测卷 题型：单选题

    如图，A，B，C三点在已知的圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是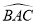的中点，连接DB，DC，则∠DBC的度数为（   ）

    A. 30° B. 45° C. 50° D. 70°

    C 【解析】在△ABC中，∠ABC=70°，∠ACB=30°，∴∠A=180°-∠ABC-∠ACB=80°， ∴∠BDC=∠A=80°， ∵D是 的中点，∴，∴∠DBC=∠DCB， ∵∠D+∠DBC+∠DCB=180°， ∴∠DBC=50°， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

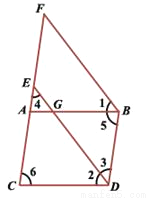
    已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．

    证明见解析. 【解析】试题分析：因为∠3=∠4，所以CA∥BD，由两直线平行，同旁内角互补可得∠6+∠2+∠3 = 180°，又因∠6 =∠5，∠2 =∠1，根据等量代换可得∠5+∠1+∠3 = 180°，从而根据同旁内角互补，两直线平行得出ED∥FB． 试题解析： ∵ ∠3 =∠4,∴ AC∥BD.∴ ∠6+∠2+∠3 = 180° ∵ ∠6 =∠5，∠2 =∠1,∴ ∠...

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册 第1-3章 综合测试卷 题型：填空题

    将线段AB平移1cm，得到线段A′B′，则点A到点A′的距离是________cm．

    1 【解析】【解析】 将线段AB平移1cm，得到线段A′B′，则点A到点A′的距离是1cm．故答案为：1．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册 第1-3章 综合测试卷 题型：填空题

    点P（a﹣1，a2﹣9）在x轴负半轴上，则P点坐标是________．

    （﹣4，0） 【解析】【解析】 由题意得：a2-9=0且a-1＜0，解得：a=-3．故答案为：（-4，0）．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册 第1-3章 综合测试卷 题型：单选题

    体育课上，七年级某班49名同学在操场上练习正方形方队，他们站成7×7方队，每横队7人，每纵队7人，小敏在第2纵队的排头，记为（1，2），小娟在第5纵队的队尾，则小娟的位置应记为（    ）

    A. （6，5） B. （5，6） C. （5，7） D. （7，5）

    D 【解析】【解析】 小娟在第5纵队的队尾，则小娟的位置应记为（7，5）．故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：填空题

    已知x为正整数，当时x=________时，分式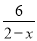的值为负整数．

    3、4、5、8 【解析】由题意得：2﹣x＜0，解得x＞2，又因为x为正整数，讨论如下： 当x=3时， =﹣6，符合题意； 当x=4时， =﹣3，符合题意； 当x=5时， =﹣2，符合题意； 当x=6时， =﹣，不符合题意，舍去； 当x=7时， =﹣，不符合题意，舍去； 当x=8时， =﹣1，符合题意； 当x≥9时，﹣1＜＜0，不符合题意．故x的值为3...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：单选题

    不等式组的解集在数轴上表示正确的是（　　）

    A. B.

    C. D.

    A 【解析】解不等式，得：x>-1， 解不等式，得：x≤2， 所以不等式组的解集为：-1

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：单选题

    如图，矩形ABCD中，已知点M是线段AB的黄金分割点，且AM＞BM，AD=AM，FB=BM，EF和GM把矩形ABCD分成四个小矩形，其面积分别用S1，S2，S3，S4表示，EF与MG相交与点N，则以下结论正确的有（　　）

    ①N是GM的黄金分割点 ②S1=S4③．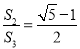

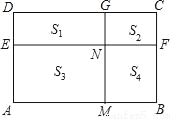
    A. ①② B. ①③ C. ③ D. ①②③

    A 【解析】因为四边形ABCD是矩形,AM=AD,BM=BF, 所以四边形AMGD,四边形BMNF都是正方形, 所以AM=AD=MG=BC,MB-BF=MN=FN, 因为点M是线段AB的黄金分割点,AM>BM, 所以, 所以, 所以,故②正确, 所以, 所以N是GM的黄金分割点,故①正确, 因为, 因为, 所以,故③错误, ...

    查看答案和解析>>

    同步练习册答案