
多项式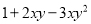 的次数及最高次项的系数分别是( )
的次数及最高次项的系数分别是( )
A. 3,-3 B. 2,-3 C. 5,-3 D. 2,3
A 【解析】根据多项式的次数是多项式中次数最高的单项式的次数,多项式1+2xy?3xy²的次数是3,最高次项的系数是?3; 故选A.科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:单选题
下列式子正确的是( )
A. 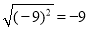 B.
B. 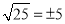
C. 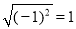 D.
D. 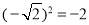
查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:单选题
如图,CD是⊙O的弦,O是圆心,把⊙O的劣弧沿着CD对折,A是对折后劣弧上的一点,∠CAD=100°,则∠B的度数是( )
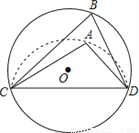
A. 100° B. 80° C. 60° D. 50°
B 【解析】试题分析:如图,翻折△ACD,点A落在A′处,可知∠A=∠A′=100°,然后由圆内接四边形可知∠A′+∠B=180°,解得∠B=80°. 故选:B查看答案和解析>>
科目:初中数学 来源:四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷(含答案) 题型:解答题
某巡警骑摩托车在一条南北大道上来回巡逻,一天早晨,他从岗亭出发,中午停留在 处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
(1) 处在岗亭何方?距离岗亭多远?
处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油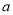 升,这一天上午共耗油多少升?
升,这一天上午共耗油多少升?
查看答案和解析>>
科目:初中数学 来源:四川省西昌市航天学校2017-2018学年七年级上册数学期中测试卷(含答案) 题型:填空题
圆周率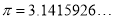 ,取近似值
,取近似值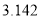 ,是精确到____位.
,是精确到____位.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:解答题
加工一批零件,由一个人做需要100小时,现在计划先由若干人做2小时,再增加5人做9小时,恰好完成任务.假设这些人的工作效率相同,求先做2小时的人数有多少?
先做2小时的人数有5人. 【解析】试题分析: 由“加工一批零件,由一个人做需要100小时”可知,1个人1小时可完成整个任务的 ,若设先做2小时的有人,则他们在2小时内完成了整个任务的: ;增加5人后的9小时完成了整个任务的: ,由此可列出方程,解方程即可得到答案; 试题解析: 设先做2小时的有人,根据题意可得: 解此方程得: . 答:先做2小时有5人. ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:填空题
一轮船航行在A、B两码头之间,已知水流速度是3千米/时,轮船顺流航行需要5小时,逆流航行需要8小时,则轮船在静水中的速度为 千米/时.
13 【解析】设轮船在静水中的速度为千米/小时,根据题意得: 解此方程得: ,即轮船在静水中的速度为:13千米/小时.查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:解答题
如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
(1)171;(2)最大值是67876,最小值是21012 【解析】试题分析:(1)设“阶梯数”t的百位为x,相邻两数的差为k,则t=,可得M=a+a=2a,N=a+k,根据P(t)=12,得到关于k的方程,可求得k=6,再根据Q(t)=3a+6为一个完全平方数,其中1≤a≤9,可求3a+6=9,16,25,可求a=1,从而得到这个三位数; (2)设某五位阶梯数为,根据==2778a+...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级浙教版数学试卷(A卷) 题型:单选题
如图所示,∠α+∠β=90°,∠β+∠γ=90°,则( ).
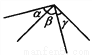
A. ∠α=β B. ∠β=∠γ C. ∠α=∠β=∠γ D. ∠α=∠γ
D 【解析】【解析】 ∠α+∠β=90°①,∠β+∠γ=90°②,①-②得:∠α-∠γ=0,∴∠α=∠γ,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com