
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出I辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.求每辆A型车和B型车的售价各为多少元.
每辆A型车的售价为18万元,B型车的售价为26万元 【解析】试题分析:设每辆A型车的售价为x元,B型车的售价为y元,根据周售出I辆A型车和3辆B型车,销售额为96万元;售出2辆A型车和1辆B型车,销售额为62万元.列出方程组解答即可. 【解析】 设每辆A型车的售价为x万元,B型车的售价为y万元,由题意得 , 解得: . 答:每辆A型车的售价为18万元,B型车的售价为... 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
小莎喜欢剪纸,某天看到了一扇漂亮的窗户(如图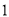 ),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图
),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图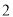 ,长方形的长是
,长方形的长是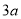 ,宽是
,宽是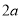 )来剪成类似的窗户纸片(如图
)来剪成类似的窗户纸片(如图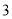 ,半圆的直径是
,半圆的直径是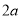 ).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含
).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含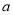 的代数式表示,保留
的代数式表示,保留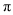 ).
).



查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期期中数学 题型:解答题
温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地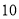 台,杭州厂可支援外地
台,杭州厂可支援外地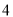 台.现在决定给武汉
台.现在决定给武汉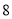 台,南昌
台,南昌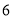 台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为
台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为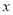 台.
台.
南昌 | 武汉 | |
温州厂 |
|
|
杭州厂 |
|
|
(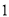 )用
)用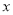 的代数式来表示总运费(单位:百元).
的代数式来表示总运费(单位:百元).
(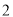 )若总运费为
)若总运费为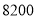 元,则杭州运往南昌的机器应为多少台?
元,则杭州运往南昌的机器应为多少台?
(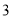 )试问有无可能使总运费是
)试问有无可能使总运费是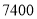 元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期期中数学 题型:单选题
下列说法正确结论的序号是( ).
(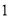 )
)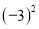 的算术平方根是
的算术平方根是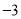 ; (
; (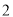 )
)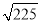 平方根是
平方根是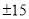 ;
;
(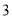 )当
)当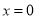 或
或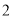 时,
时, 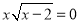 ; (
; (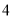 )
)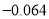 的立方根是
的立方根是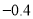 .
.
A. (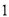 )(
)(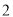 )(
)(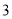 )(
)(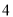 ) B. (
) B. (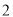 )(
)(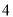 )
)
C. (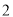 )(
)(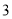 )(
)(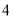 ) D. (
) D. (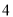 )
)
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第5讲 一次方程(组)的解法及应用 题型:填空题
已知派派的妈妈和派派今年共36岁,再过5年,派派的妈妈的年龄比派派年龄的4倍还大1岁.当派派的妈妈40岁时,派派的年龄为________岁.
12 【解析】【解析】 设今年派派的年龄为x岁,则妈妈的年龄为(36﹣x)岁,根据题意得: 36﹣x+5=4(x+5)+1,解得:x=4,∴36﹣x﹣x=28,∴40﹣28=12(岁).故答案为:12.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第5讲 一次方程(组)的解法及应用 题型:单选题
(2017衢州)二元一次方程组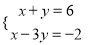 的解是( )
的解是( )
A. 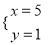 B.
B. 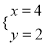 C.
C. 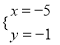 D.
D. 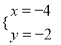
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第二十章达标检测卷 题型:解答题
如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:km/h).
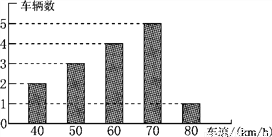
(1)计算这些车的平均速度.
(2)车速的众数是多少?
(3)车速的中位数是多少?
(1)60 km/h;(2)70 km/h;(3)60 km/h 【解析】试题分析:(1)根据频数分布直方图,利用加权平均数的定义可求得;(2)因为出现次数最多的数据是一组数据的众数,所以众数是70;(3)将一组数据按照从小到大的顺序排列,当有奇数个数据时,中位数是最中间的数据,当有偶数个数据时,中位数是最中间的两个数据的平均数. 试题解析:(1)这些车的平均速度是:(40×2+50×...查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017七年级数学上期期末试卷 题型:解答题
(8分) 如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
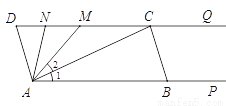
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
(1)见解析;(2) ∠CAN=50°;(3)①不会, ∠AMD:∠ACD=2;②∠ACB=75°. 【解析】试题分析:(1)由平行线的性质和判定即可得到结论; (2)由角平分线的定义和角的和差可以得到结论; (3)①不会.根据平行线的性质即可得到结论; ②由平行线的性质和∠AND=∠ACB,得到∠NAB=∠DAC,进而得到∠1=∠DAN,即可得到结论. 试题解析:【...查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:单选题
如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
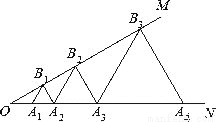
A. 8 B. 16 C. 24 D. 32
B 【解析】如图所示: ∵△A1B1A2是等边三角形, ∴A1B1=A2B1,∠3=∠4=∠12=60°, ∴∠2=120°, ∵∠MON=30°, ∴∠1=180°﹣120°﹣30°=30°, 又∵∠3=60°, ∴∠5=180°﹣60°﹣30°=90°, ∵∠MON=∠1=30°, ∴OA1=A1B1=1, ∴A2B1=1, ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com