
小莎喜欢剪纸,某天看到了一扇漂亮的窗户(如图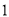 ),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图
),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图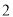 ,长方形的长是
,长方形的长是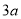 ,宽是
,宽是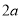 )来剪成类似的窗户纸片(如图
)来剪成类似的窗户纸片(如图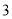 ,半圆的直径是
,半圆的直径是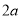 ).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含
).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含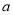 的代数式表示,保留
的代数式表示,保留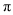 ).
).



 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源:浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型:解答题
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
收费标准(注:水费按月份结算) | |
每月用水量 | 单价(元/立方米) |
不超出 |
|
超出 |
|
超出 |
|
例如:某户居民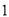 月份用水
月份用水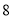 立方米,应收水费为
立方米,应收水费为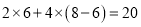 (元).
(元).
请根据上表的内容解答下列问题:
(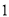 )若某户居民
)若某户居民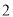 月份用水
月份用水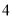 立方米,则应收水费多少元?
立方米,则应收水费多少元?
(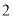 )若某户居民
)若某户居民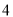 月份用水
月份用水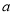 立方米(其中
立方米(其中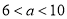 ),请用含
),请用含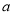 的代数式表示应收水费.
的代数式表示应收水费.
(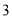 )若某户居民
)若某户居民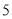 、
、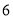 两个月共用水
两个月共用水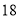 立方米(
立方米(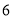 月份用水量超过了
月份用水量超过了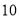 立方米),设
立方米),设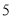 月份用水
月份用水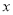 立方米,请用含
立方米,请用含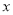 的代数式表示该居民
的代数式表示该居民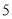 、
、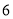 两个月共交水费多少元.
两个月共交水费多少元.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:填空题
平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=________.
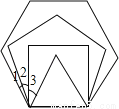
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
已知如图,在数轴上点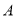 ,
, 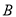 所对应的数是
所对应的数是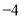 ,
, 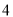 .
.
对于关于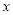 的代数式
的代数式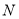 ,我们规定:当有理数
,我们规定:当有理数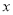 在数轴上所对应的点为
在数轴上所对应的点为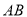 之间(包括点
之间(包括点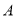 ,
, 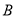 )的任意一点时,代数式
)的任意一点时,代数式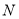 取得所有值的最大值小于等于
取得所有值的最大值小于等于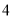 ,最小值大于等于
,最小值大于等于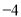 ,则称代数式
,则称代数式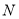 ,是线段
,是线段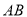 的封闭代数式.
的封闭代数式.
例如,对于关于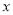 的代数式
的代数式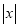 ,当
,当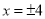 时,代数式
时,代数式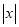 取得最大值是
取得最大值是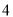 ;当
;当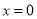 时,代数式
时,代数式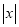 取得最小值是
取得最小值是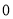 ,所以代数式
,所以代数式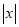 是线段
是线段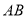 的封闭代数式.
的封闭代数式.
问题:(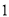 )关于
)关于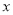 代数式
代数式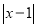 ,当有理数
,当有理数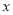 在数轴上所对应的点为
在数轴上所对应的点为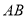 之间(包括点
之间(包括点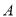 ,
, 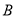 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.
所以代数式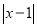 __________(填是或不是)线段
__________(填是或不是)线段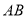 的封闭代数式.
的封闭代数式.
(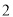 )以下关
)以下关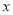 的代数式:
的代数式:
①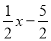 ;②
;②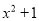 ;③
;③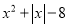 ;④
;④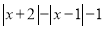 .
.
是线段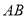 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段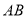 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).
(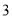 )关于
)关于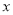 的代数式
的代数式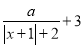 是线段
是线段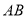 的封闭代数式,则有理数
的封闭代数式,则有理数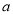 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
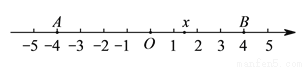
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
计算: 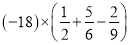 .
.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题

A. 汉城与纽约的时差为13小时
B. 汉城与多伦多的时差为13小时
C. 北京与纽约的时差为14小时
D. 北京与多伦多的时差为14小时
B 【解析】试题分析:理解两地国际标准时间的差简称为时差.根据有理数减法法则计算,减去一个数等于加上这个数的相反数.因此可求汉城与纽约的时差为9﹣(﹣5)=14小时;汉城与多伦多的时差为9﹣(﹣4)=13小时;北京与纽约的时差为8﹣(﹣5)=13小时;北京与多伦多的时差为8﹣(﹣4)=12小时. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区2016-2017学年七年级上学期期末数学试卷 题型:填空题
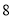 的立方根为__________,
的立方根为__________, 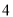 的平方根为__________.
的平方根为__________.
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第5讲 一次方程(组)的解法及应用 题型:解答题
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出I辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.求每辆A型车和B型车的售价各为多少元.
每辆A型车的售价为18万元,B型车的售价为26万元 【解析】试题分析:设每辆A型车的售价为x元,B型车的售价为y元,根据周售出I辆A型车和3辆B型车,销售额为96万元;售出2辆A型车和1辆B型车,销售额为62万元.列出方程组解答即可. 【解析】 设每辆A型车的售价为x万元,B型车的售价为y万元,由题意得 , 解得: . 答:每辆A型车的售价为18万元,B型车的售价为...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com