
如图,是一个正方体的表面展开图,则原正方体中与“国”字所在的面相对的面上标的字是( )

A. 伟 B. 人 C. 的 D. 梦
A 【解析】这是一个正方体的平面展开图,共有六个面,其中面“梦”与面“伟”相对,面“大”与面“中”相对,面“国”与面“的”相对。 故选:A.科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:单选题
随着计算机技术的迅猛发展,电脑价格不断降低,某品牌的电脑按原价降低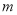 元后又降20%,现售价为
元后又降20%,现售价为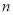 元,那么该电脑的原售价为 ( )
元,那么该电脑的原售价为 ( )
A. 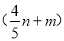 元 B.
元 B. 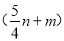 元 C.
元 C. 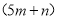 元 D.
元 D. 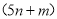 元
元
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
在平面内,正方形ABCD与正方形CEFH如图放置,连接DE,BH,两线交于M,求证:
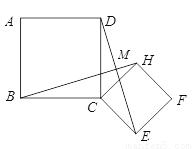
(1)BH=DE;
(2)BH⊥DE.
(1)证明见解析(2)证明见解析 【解析】试题分析:(1)根据正方形的性质可得BC=CD,CE=CH,∠BCD=∠ECH=90°,然后求出∠BCH=∠DCE,再利用“边角边”证明△BCH和△DCE全等,根据全等三角形对应边相等证明即可; (2)根据全等三角形对应角相等可得∠CBH=∠CDE,然后根据三角形的内角和定理求出∠DMB=∠BCD=90°,再根据垂直的定义证明即可. 试题...查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
数轴上点A、B、C的位置如图所示,A、B对应的数分别为?5和1,已知线段AB的中点D与线段BC的中点E之间的距离为5.
(1)求点D对应的数;
(2)求点C对应的数.
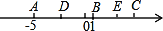
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:填空题
把一根木条固定在墙上至少需要钉_______颗钉子,根据是_____________.
2 两点可以确定一条直线; 【解析】∵两点确定一条直线, ∴要把木条固定在墙上至少需要钉2颗钉子. 故答案为:2,两点确定一条直线.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
据初步统计,2015年北仑区实现地区生产总值(GDP)约为1134.6亿元.其中1134.6亿元用科学记数法表示为( )
A.1134.6×108元 B.11.346×1010元
C.1.1346×1011元 D.1.1346×1012元
C 【解析】 试题分析:1134.6亿用科学记数法表示应为:1.1346×1011查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图 ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” 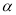 约为
约为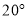 ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”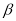 约为
约为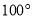 .图
.图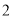 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线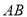 水平,且与屏幕
水平,且与屏幕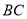 垂直.
垂直.

( )若屏幕上下宽
)若屏幕上下宽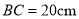 ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离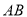 的长.
的长.
( )若肩膀到水平地面的距离
)若肩膀到水平地面的距离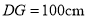 ,上臂
,上臂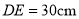 ,下臂
,下臂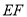 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离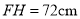 ,请判断此时
,请判断此时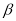 是否符合科学要求的
是否符合科学要求的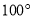 ?
?
(参考数据: 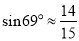 ,
, 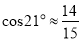 ,
, 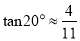 ,
, 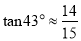 ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,用20m的篱笆围成一个矩形的花圃.设连墙的一边为x(m),矩形的面积为y(m2).

(1)写出y关于x的函数解析式;
(2)当x=3时,矩形的面积为多少?
(1)y=﹣2x2+20x;(2)42 【解析】试题分析:(1)设连墙的一边为x(m),矩形的面积为y(m2),则另一边长为:(20-2x)m,根据矩形面积公式写出函数关系式即可;(2)将x=3代入函数解析式求出y即可. 试题解析: (1)设连墙的一边为x(m),矩形的面积为y(m2), 则另一边长为:(20-2x)m, ∴y关于x的函数解析式为:y=x(20-2x)=-2...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:单选题
如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;④ 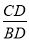 =1.其中正确的是( )
=1.其中正确的是( )
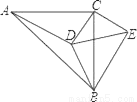
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
D 【解析】试题分析:①根据:∠CAD=30°,AC=BC=AD,利用等腰三角形的性质和三角形内角和定理即可求出∠ECA=165°,从而得证结论正确; ②根据CE⊥CD,∠ECA=165°,利用SAS求证△ACD≌△BCE即可得出结论; ③根据∠ACB=90°,∠CAD=30°,AC=BC,利用等腰三角形的性质和△ACD≌△BCE,求出∠CBE=30°,然后即可得出结论; ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com