
古代埃及人在进行分数运算时,只使用分子是1的分数,因此这种分数也叫做埃及分数.我们注意到,某些真分数恰好可以写成两个埃及分数的和,例如: 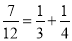 .
.
(1)请将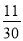 写成两个埃及分数的和的形式_______________;
写成两个埃及分数的和的形式_______________;
(2)若真分数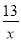 可以写成两个埃及分数和的形式,请写出两个
可以写成两个埃及分数和的形式,请写出两个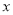 不同的取值_________.
不同的取值_________.
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:填空题
如图,在半径为5cm的⊙O中,如果弦AB的长为8cm,OC⊥AB,垂足为C,那么OC的长为____________cm.

查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
作图题:如图,已知平面上四点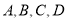 .
.

(1)画直线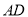 ;
;
(2)画射线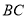 ,与直线
,与直线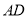 相交于
相交于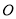 ;
;
(3)连结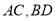 相交于点
相交于点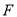 .
.
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
将“富强、民主、文明”六个字分别写在一个正方体的六个面上,正方体的平面展开图如图所示,那么在这个正方体中,和“强”相对的字是( )

A. 文 B. 明 C. 民 D. 主
A 【解析】试题分析:这是一个正方体的平面展开图,共有六个面,其中面“强”与面“文”相对,面“富”与面“主”相对,“民”与面“明”相对. 故选A.查看答案和解析>>
科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:解答题
如图所示,点A,O,B在同一条直线上,∠BOC=40°,射线OC⊥射线OD,射线OE平分∠AOC.求∠DOE的大小.
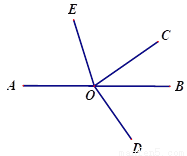
查看答案和解析>>
科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:填空题
若∠1=35°21′,则∠1的余角是 。
54°39′. 【解析】 试题解析:根据定义,∠1的余角度数是90°-35°21′=54°39′.查看答案和解析>>
科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:单选题
中国古代人民很早就在生产生活种发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有x辆车,则可列方程( )
A. 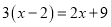 B.
B. 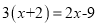 C.
C. 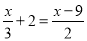 D.
D. 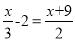
查看答案和解析>>
科目:初中数学 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:填空题
如果一个正多边形每一个内角都等于144°,那么这个正多边形的边数是_________.
10 【解析】设这个多边形的边数为n,则有 180(n-2)=144n, 解得:n=10, 故答案为:10.查看答案和解析>>
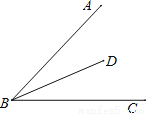
科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:解答题
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com