练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    单项式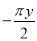的系数是_________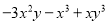； 是__________次多项式．

    - , 4 【解析】【解析】 单项式的系数是； 是4次多项式．故答案为： ，4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省绵阳市三台县2018届九年级（上）第一学月数学试卷 题型：单选题

    如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…，第n行有n个点…，若该三角点阵前n行的点数和为300，则n的值为（　　）

    A. 30 B. 26 C. 25 D. 24

    D 【解析】由题意得： n（n+1）=300 解得：n=24． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（华师大版）：期中检测题 题型：填空题

    中国古代的数学专著《九章算术》有方程组问题“五只雀，六只燕，共重1斤(等于16两)，雀重燕轻．互换其中一只，恰好一样重．”设每只雀、燕的重量各为x两，y两，则根据题意，可得方程组为___．

    【解析】设每只雀、燕的重量各为x两，y两，由题意得： 故答案是： 或 。

    查看答案和解析>>

    科目：初中数学 来源：内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    广州亚运会中，志愿者们手上、脖子上的丝巾非常美丽，车间70名工人承接了生产丝巾的任务，已知每人每天平均生产手上的丝巾1800条或脖子上的丝巾1200条，一条脖子上的丝巾要配两条手上的丝巾，为了使每天生产的丝巾正好配套，应分配多少名工人生产脖子上的丝巾，多少名工人生产手上的丝巾？

    应分配30名工人生产脖子上的丝巾，40名工人生产手上的丝巾． 【解析】试题分析：设应分配名工人生产脖子上的丝巾，则（70-x）名工人生产手上的丝巾，根据一条脖子上的丝巾要配两条手上的丝巾列方程. 试题解析：【解析】 设应分配名工人生产脖子上的丝巾， 则：， 解得：， ， 答：应分配30名工人生产脖子上的丝巾，40名工人生产手上的丝巾．

    查看答案和解析>>

    科目：初中数学 来源：内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    换算：65.24°＝_____度_____分_____秒．

    65， 14 24, 【解析】【解析】 65.24°=65°14′24″．故答案为：65，14，24．

    查看答案和解析>>

    科目：初中数学 来源：内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    关于x的方程2（x﹣1）﹣a=0的根是3，则a的值为（ ）

    A．4 B．﹣4 C．5 D．﹣5

    A 【解析】 试题分析：虽然是关于x的方程，但是含有两个未知数，其实质是知道一个未知数的值求另一个未知数的值． 【解析】 把x=3代入2（x﹣1）﹣a=0中： 得：2（3﹣1）﹣a=0 解得：a=4 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市2017-2018学年七年级上学期第三次月考数学试卷 题型：解答题

    如图，已知数轴上点A表示的数为a，点B表示的数为b，且满足．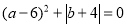

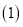    写出a、b及AB的距离：

    ______   ______   ______

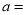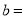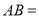    若动点P从点A出发，以每秒6个单位长度沿数轴向左匀速运动，动点Q从点B出发，以每秒4个单位长度向左匀速运动．

    若P、Q同时出发，问点P运动多少秒追上点Q？

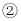    若M为AP的中点，N为PB的中点，点P在运动过程中，线段MN是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长．

    （1）6； ；10；（2）①点P运动5秒时追上点Q②线段MN不发生变化 【解析】试题分析：(1)根据非负数的性质可得a-6=0,b+4=0,计算出a、b的值,然后可计算出AB的长度; (2)①设点P运动t秒时追上点Q,根据题意可得等量关系:点P运动的路程-点Q运动的路程,根据等量关系列出方程,再解即可; ②此题要分两种情况:当P在线段AB之间时;当P在线段AB的延长线上时,分别画出图...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市2017-2018学年七年级上学期第三次月考数学试卷 题型：填空题

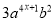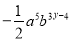    如果单项式与可以合并为一项，那么x与y的值应分别为______________ ．

    【解析】∵单项式与可以合并为一项， ∴单项式与是同类项， ∴4x+1=5,3y-4=2, ∴x=1,y=2.

    查看答案和解析>>

    科目：初中数学 来源：四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型：填空题

    如图，在平面直角坐标系中，菱形ABCD在第一象限内，AB=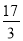，对角线BD与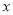轴平行，B，C两点的横坐标分别为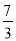、5，反比例函数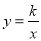的图象经过B，C两点，则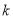的值为___________．

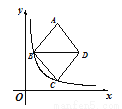
    【解析】试题分析：连接AC与BC相交于点O， ∵四边形ABCD是菱形， ∴AC⊥BD，BC＝AB＝， ∵对角线BD与轴平行，B，C两点的横坐标分别为、5， ∴BO＝5－＝， 在Rt△BOC中， OC＝＝＝5， ∵B、C在y＝图象上， ∴yB＝，yC＝， ∴OC＝ yB － yC ＝－＝5， 解得k＝． 故答案为．

    查看答案和解析>>

    同步练习册答案