
ijУ�ƻ�����ס����������繲1000�������̻�У����������ÿ��25Ԫ����������ÿ��30Ԫ��ͨ�������˽⣬�ף�����������ɻ��ʷֱ���90%��95%��
��1���������������繲��ȥ28000Ԫ����ס��������������������ꣿ
��2��Ҫʹ����������ܳɻ��ʲ�����92%�������������������ꣿ
��3���ڣ�2���������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
��1������������400�꣬��������600�ꣻ��2��������������600�ꣻ��3�������������600�꣮��������400��ʱ�ܷ�����ͣ���ͷ���Ϊ27000Ԫ�� �������������������1���������Ӧ�ý���ؼ������δ֪�����ҳ�������ϵ���г���������⣮�����蹺��������x�꣬��������y�꣬���ݹ���ס����������繲1000���������������ܼ�Ϊ28000Ԫ���������������⼴�ɣ� ��2������...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����������2016-2017ѧ�����ѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ������
��a+b=8��ab=-5,��(a-b)2��___________.
84 �������������������a+b=8����ƽ���ã���a+b��2=a2+b2+2ab=64�� ��ab=-5����ã�a2+b2=74�� ��ԭʽ=a2+b2-2ab=74+10=84�� �ʴ�Ϊ��84�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ��ׯ���п���ѧģ���Ծ� ���ͣ������
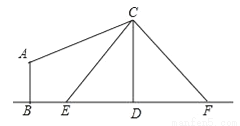
��ͼ�����߸�CD�ϵ�C��������CE��CF�̶����߸ˣ�������߸�6��B�����ò���ǣ���B��E��D��ͬһֱ���ϣ�����A����õ��߸���C��������Ϊ30�㣬��֪����ǵĸ�AB=1.5�ף�BE=2.3�ף�������CE�ij�������ȷ��0.1�ף��ο�����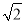 ��1.41��
��1.41��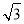 ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ��ׯ���п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��������������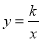 ��x��0����ͼ����һ��A��AB��x���ڵ�B������AO����S��AOB=2����k��ֵΪ�� ��
��x��0����ͼ����һ��A��AB��x���ڵ�B������AO����S��AOB=2����k��ֵΪ�� ��
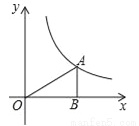
A. 2 B. 3 C. 4 D. 5
C ������������������ߵ�A�Ƿ���������ͼ����һ�㣬��AB��x���ڵ�B����S��AOB=|k|=2����ã�k=��4�� �߷����������ڵ�һ������ͼ��k=4����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ��ׯ���п���ѧģ���Ծ� ���ͣ���ѡ��
��ʽ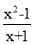 ��ֵΪ�㣬��x��ֵΪ��������
��ֵΪ�㣬��x��ֵΪ��������
A. ��1 B. 0 C. ��1 D. 1
D ��������������� ��֮�� x=1. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŶ�����˹�ж��п�����꼶���£���ĩ��ѧ�Ծ� ���ͣ������
���㣺(1) 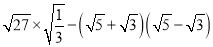
��2��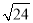 ��
��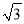 ��4��
��4��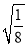 ����1��
����1�� ) 0
) 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŶ�����˹�ж��п�����꼶���£���ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ��������ABCD�ı߳�Ϊ2cm������P�ӵ�A�������������εı�����A��B��C�ķ����˶�����Cֹͣ�����P���˶�·��Ϊx��cm��������ͼ���У���ʾ��ADP�����y��cm2������x��cm���ĺ�����ϵ��ͼ���ǣ�������
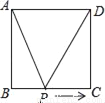
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ��� ���ͣ������
�������ɷ�Ϊ�������������������࣮_____���ж϶Դ���
���� �����������������Է�Ϊ����������0��������������. �ʴ�Ϊ����.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�ϳ���Ӫɽ�س��϶�С2017-2018ѧ����ѧ�ھ��꼶��ѧ��ĩ��������Ծ� ���ͣ������
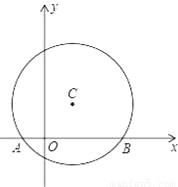
����ͼ����ƽ��ֱ������ϵ�У��Ե�C��1��1��ΪԲ�ģ�2Ϊ�뾶��Բ����x����A��B���㣬��P���Ż�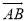 �ϣ�
�ϣ�
��1�����A��B��������ꣻ
��2����ȷ������A��B���Ե�PΪ����������߽���ʽ��
��3���ڸ����������Ƿ����һ��D��ʹ�߶�OP��CD����ƽ�֣������ڣ������D�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com