练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若，那么下列等式不一定成立的是（ 　）

    A. B. C. D.

    B 【解析】试题解析： 时， 不一定成立.故错误. 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型：解答题

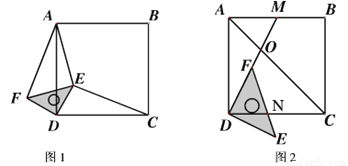
    已知:正方形ABCD，等腰直角三角板的直角顶点落在正方形的顶点D处，使三角板绕点D旋转.

    (1)当三角板旋转到图1的位置时，猜想CE与AF的数量关系，并加以证明；

    (2)在(1)的条件下，若DE:AE:CE= 1: 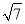:3，求∠AED的度数；

    (3)若BC= 4，点M是边AB的中点，连结DM，DM与AC交于点O，当三角板的一边DF与边DM重合时(如图2)，若OF=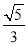，求CN的长.

    （1）CE=AF；证明见解析；（2）135°；（3）. 【解析】试题分析： （1）由正方形额等腰直角三角形的性质判断出△ADF≌△CDE即可； （2）设DE=k，表示出AE，CE，EF，判断出△AEF为直角三角形，即可求出∠AED； （3）由AB∥CD，得出，求出DM，DO，再判断出△DFN∽△DCO，得到 ，求出DN即可． 试题解析： （1）CE=AF； ...

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型：单选题

    已知点C在线段AB上，则下列条件中，不能确定点C是线段AB中点的是（　　）

    A. AC=BC B. AB=2AC C. AC+BC=AB D. BC=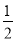AB

    C 【解析】试题分析：A、AC＝BC，则点C是线段AB中点； B、AB＝2AC，则点C是线段AB中点； C、AC＋BC＝AB，则C可以是线段AB上任意一点； D、BC＝AB，则点C是线段AB中点． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县2017-2018学年七年级上期末统一质量检测数学试卷 题型：解答题

    计算: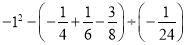

    -12. 【解析】试题分析：按照有理数的运算顺序运算即可. 试题解析：原式

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县2017-2018学年七年级上期末统一质量检测数学试卷 题型：填空题

    小红在写作业时，不慎将一滴墨水滴在数轴上，根据图中的数据，请确定墨迹遮盖住的整数共有____个．

    3 【解析】试题解析： 被墨迹遮盖住的整数有： 共3个. 故答案为：3.

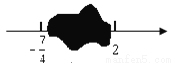
    查看答案和解析>>

    科目：初中数学 来源：上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型：解答题

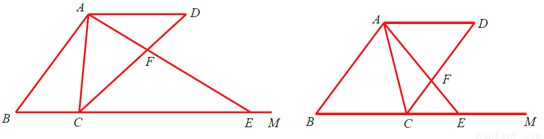
    已知AB=5，AD=4，AD∥BM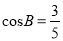， （如图），点C、E分别为射线BM上的动点（点C、E都不与点B重合），联结AC、AE，使得∠DAE=∠BAC，射线EA交射线CD于点F．设BC=x， ．

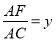    （1）如图1，当x=4时，求AF的长；

    （2）当点E在点C的右侧时，求y关于x的函数关系式，并写出函数的定义域；

    （3）联结BD交AE于点P，若△ADP是等腰三角形，直接写出x的值．

    （1）；（2）；（3）或或． 【解析】分析：作AH⊥BC于H，如图1，利用余弦的定义和勾股定理计算出BH=3，AH=4，AC=，再判断四边形ABCD为平行四边形得到∠B=∠D，接下来证明△ADF∽△ABC，然后利用相似比计算出AC；（2）如图2，先证明△BAC∽△BEA,利用相似比得到BE=,AC= ,则CE= ，再证明△ADF∽EFC,利用相似比得到AF= ,然后计算AF·AC可得到y与x...

    查看答案和解析>>

    科目：初中数学 来源：上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型：填空题

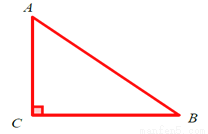
    在Rt△ABC中，∠C=90°，AC=6，BC=8（如图），点D是边AB上一点，把△ABC绕着点D旋转90°得到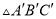，边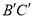与边AB相交于点E，如果AD=BE，那么AD长为____．

    ． 【解析】在Rt△ABC中， 由旋转的性质，设AD=A′D=BE=x，则DE=2x-10， ∵△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′， ∴∠A′=∠A，∠A′DE=∠C=90°， ∴∽△BCA，∴ , ∵=10-x, ∴ , ∴x= ,故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型：单选题

    如果两个相似三角形对应边之比是1：3，那么它们的对应中线之比是（　　　）

    A. 1：3 B. 1：4 C. 1：6 D. 1：9

    A 【解析】∵两个相似三角形对应边之比是1:3， ∴它们的对应中线之比为1:3. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（　　）

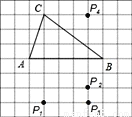
    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】要使△ABP与△ABC全等，必须使点P到AB的距离等于点C到AB的距离，即3个单位长度，所以点P的位置可以是P1，P3，P4三个，故选C.

    查看答案和解析>>

    同步练习册答案