
将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )
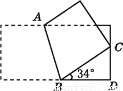
A. 73° B. 56° C. 68° D. 146°
A 【解析】试题分析:根据补角的知识可求出∠CBE,从而根据折叠的性质∠ABC=∠ABE=∠CBE,可得出∠ABC的度数. ∵∠CBD=34°, ∴∠CBE=180°﹣∠CBD=146°, ∴∠ABC=∠ABE=∠CBE=73°.科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
下列调查中,最适合采用全面调查(普查)方式的是( )
A. 对重庆市辖区内长江流域水质情况的调查
B. 对乘坐飞机的旅客是否携带违禁物品的调查
C. 对一个社区每天丢弃塑料袋数量的调查
D. 对重庆电视台“天天630”栏目收视率的调查
B 【解析】选项A,水量众多,应选用抽样调查;选项B,人数不多,意义重大,应选用全面调查;选项C,数量较多,工作量大,易采用抽样调查;选项D,人数众多,意义不大,因此应选择抽样调查;故选B.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,正六边形ABCDEF的内切圆和外接圆半径之比为_________.
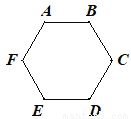
查看答案和解析>>
科目:初中数学 来源:浙江省2017学年第一学期七年级期末检测数学试卷卷 题型:解答题
解方程: (1)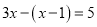 (2)
(2) 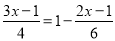
查看答案和解析>>
科目:初中数学 来源:浙江省2017学年第一学期七年级期末检测数学试卷卷 题型:单选题
下列四个数中,最大的一个数是( )
A.2 B.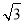 C.0 D.﹣2
C.0 D.﹣2
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
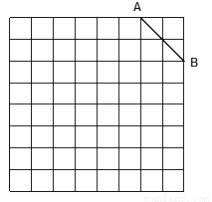
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(2,4),B点坐标为(4,2);
⑵ 请在(1)中建立的平面直角坐标系的第一象限内的格点上确定点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 , △ABC的周长是 (结果保留根号);
⑶ 以(2)中△ABC的点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
已知点P关于y轴的对称点P1的坐标是(2,3),则点P坐标是( )
A. (-3,-2) B. (-2,3) C. (2,-3) D. (3,-2)
B 【解析】试题分析:直接利用关于y轴对称点的性质得出点P坐标. 【解析】 ∵P关于y轴的对称点P1的坐标是(2,3), ∴点P坐标是:(﹣2,3). 故选:B.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
如图,在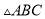 中,已知
中,已知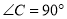 ,
, 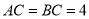 ,
, 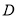 是
是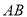 的中点,点
的中点,点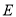 、
、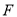 分别在
分别在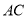 、
、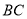 边上运动(点
边上运动(点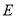 不与点
不与点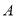 、
、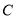 重合),且保持
重合),且保持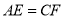 ,连接
,连接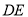 、
、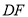 、
、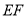 .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )
①四边形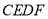 有可能成为正方形;②
有可能成为正方形;②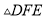 是等腰直角三角形;
是等腰直角三角形;
③四边形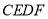 的面积是定值;④点
的面积是定值;④点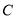 到线段
到线段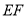 的最大距离为
的最大距离为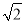 .
.
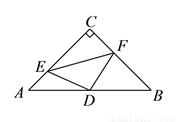
A. ①④ B. ①②③ C. ①②④ D. ①②③④
D 【解析】①当DE⊥AC,DF⊥BC时,此时四边形CEDF是矩形,由AC=BC,∠ACB=90°,则∠A=∠B=45°,由CD⊥AB,则∠ACD=∠BCD=45°,则AD=CD=BD,同理CE=AE=DE,则此时四边形CEDF是正方形,正确; ②连接CD,在△ADE和△CDF中,AE=CF, ∠A=∠DCF=45°,AD=CD, ∴△ADE≌△CDF, ∴ED=DF,∠C...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com