
��ͼ����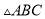 �У���֪
�У���֪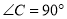 ��
�� 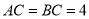 ��
�� 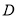 ��
��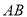 ���е㣬��
���е㣬��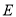 ��
��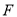 �ֱ���
�ֱ���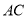 ��
��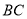 �����˶�����
�����˶����� �����
����� ��
�� �غϣ����ұ���
�غϣ����ұ���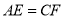 ������
������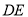 ��
��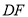 ��
��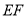 ���ڴ��˶��仯�Ĺ����У������н��ۣ�������ȷ�Ľ����ǣ� ��
���ڴ��˶��仯�Ĺ����У������н��ۣ�������ȷ�Ľ����ǣ� ��
���ı���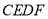 �п��ܳ�Ϊ�����Σ���
�п��ܳ�Ϊ�����Σ��� �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
���ı��� ������Ƕ�ֵ���ܵ�
������Ƕ�ֵ���ܵ� ���߶�
���߶�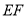 ��������Ϊ
��������Ϊ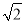 ��
��
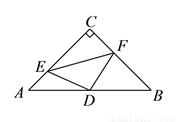
A. �٢� B. �٢ڢ� C. �٢ڢ� D. �٢ڢۢ�
D ���������ٵ�DE��AC,DF��BCʱ,��ʱ�ı���CEDF�Ǿ���,��AC=BC,��ACB=90��,���A=��B=45��,��CD��AB,���ACD=��BCD=45�㣬��AD=CD=BD,ͬ��CE=AE=DE,���ʱ�ı���CEDF�������Σ���ȷ�� ������CD���ڡ�ADE�͡�CDF�У�AE=CF, ��A=��DCF=45��,AD=CD, ���ADE�ա�CDF�� ��ED=DF����C...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ2017ѧ���һѧ�����꼶��ĩ�����ѧ�Ծ��� ���ͣ���ѡ��
��һ�ų�����ֽƬ�۵�����ͼ��ʾ����״,���ABC����(����)
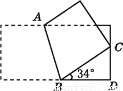
A. 73�� B. 56�� C. 68�� D. 146��
A ��������������������ݲ��ǵ�֪ʶ�������CBE���Ӷ������۵������ʡ�ABC=��ABE=��CBE���ɵó���ABC�Ķ����� �ߡ�CBD=34�㣬 ���CBE=180�㩁��CBD=146�㣬 ���ABC=��ABE=��CBE=73�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������³�������·���ʵ�������������ѧ�Ծ� ���ͣ������
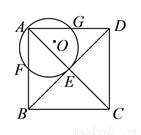
��ͼ����������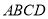 �У�
�У�  Ϊ�Խ���
Ϊ�Խ���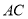 ��
�� 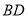 �Ľ��㣬������
�Ľ��㣬������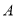 �͵�
�͵�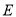 ����
����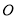 ���ֱ�
���ֱ�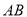 ��
�� 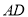 �ڵ�
�ڵ� ��
��  ����֪�����α߳�Ϊ
����֪�����α߳�Ϊ ����
����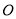 �İ뾶Ϊ
�İ뾶Ϊ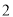 ����
����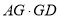 ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������ຼ��Ӣ�������ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��ͼ���ڱ߳�Ϊ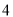 ��������
��������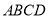 ����
����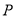 ��
��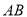 �ϴ�
�ϴ�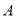 ��
��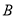 �˶�������
�˶�������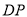 ��
��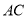 �ڵ�
�ڵ�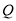 ��
��
��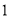 ����֤�������۵�
����֤�������۵�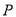 �˶���
�˶���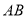 �Ϻδ�ʱ������
�Ϻδ�ʱ������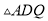 ��
��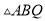 ��
��
��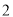 ������
������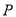 �ӵ�
�ӵ�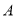 �˶�����
�˶�����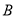 ���ټ�����
���ټ�����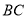 ���˶�����
���˶�����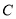 ���������˶������У���
���������˶������У���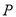 ��ÿ��
��ÿ�� ��λ���ȵ��ٶ������˶�����
��λ���ȵ��ٶ������˶����� ǡΪ���������Σ����
ǡΪ���������Σ����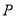 �˶���ʱ�䣮
�˶���ʱ�䣮
�鿴�𰸺ͽ���>>
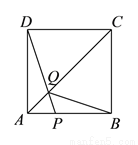
��Ŀ��������ѧ ��Դ���㽭ʡ�������ຼ��Ӣ�������ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��֪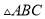 �У�
�� 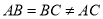 ������
������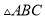 ֻ��һ�������ߣ�����
ֻ��һ�������ߣ�����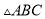 ȫ�ȵ������Σ�������������һ��������__________����
ȫ�ȵ������Σ�������������һ��������__________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������ຼ��Ӣ�������ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ���ѡ��
����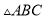 ��
�У� 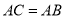 ���������߽���һ��
���������߽���һ��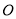 ��������
��������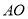 ��
��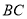 �Ĺ�ϵ��ȷ���ǣ� ����
�Ĺ�ϵ��ȷ���ǣ� ����
A. 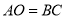 B.
B. 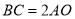 C. ��ֱ D.
C. ��ֱ D. 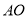 ��ֱƽ��
��ֱƽ��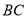
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ������
��ͼ����ƽ���ı���ABCD�У���AΪԲ�ģ�AB�ij�Ϊ�뾶��Բǡ����CD�����ڵ�C����AD�ڵ�E���ӳ�BA���A�ཻ�ڵ�F����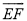 �ij�Ϊ
�ij�Ϊ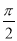 ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
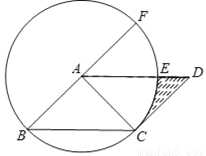
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��AB�ǡ�O���ң�AC�ǡ�O���ߣ�AΪ�е㣬BC����Բ�ģ�����B=20�㣬���C�Ĵ�С���ڣ�������
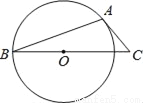
A. 20�� B. 25�� C. 40�� D. 50��
D �������������������ͼ������OA�� ��AC�ǡ�O�����ߣ� ���OAC=90�㣬 ��OA=OB�� ���B=��OAB=25�㣬 ���AOC=50�㣬 ���C=40�㣮 ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³����۳���ѧ2018����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��1��2��3��4����ȡ������ͬ��������˻�����4�ĸ����� ��
�� ��������������������ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ������˻�����4������������ø��ʹ�ʽ������ô𰸣� �������� ����״ͼ�ã� �߹���12�ֵȿ��ܵĽ������ȡ������ͬ��������˻�����4����6������� ���1��2��3��4����ȡ������ͬ��������˻�����4�ĸ����ǣ�=�� �ʴ�Ϊ�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com