
在平面直角坐标系中,点(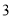 ,
, 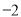 )关于
)关于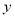 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A. (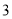 ,
, 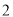 ) B. (
) B. (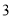 ,
, 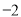 ) C. (
) C. (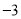 ,
, 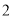 ) D. (
) D. (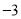 ,
, 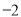 )
)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:江苏省扬州市2018届九年级12月月考数学试卷 题型:解答题
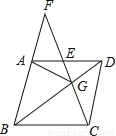
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG.
(2)求证:AG2=GE•GF.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
下列作图语句正确的是( )
A. 作射线AB,使AB=a B. 作∠AOB=∠a
C. 延长直线AB到点C,使AC=BC D. 以点O为圆心作弧
B 【解析】试题分析:根据射线、直线的延伸性以及确定弧的条件即可作出判断. 【解析】 A、射线是不可度量的,故选项错误; B、正确; C、直线是向两方无线延伸的,故选项错误; D、需要说明半径的长,故选项错误. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(A卷) 题型:填空题
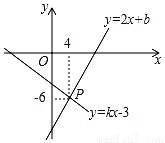
如图,已知一次函数y=2x+b和y=kx﹣3(k≠0)的图象交于点P,则二元一次方程组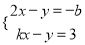 的解是_____.
的解是_____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(A卷) 题型:单选题
在某次数学测验中,某小组8名同学的成绩如下:81,73,81,81,85,83,87,89,则这组数据的中位数、众数分别为( ).
A. 80,81 B. 81,89 C. 82,81 D. 73,81
C 【解析】试题解析:将这组数从小到大排列为73,81,81,81,83,85,87,89,观察数据可知,最中间的那两个数为81和83,则中位数为82,而81出现的次数最多,所以众数是81.故本题应选C.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌云县2017-2018学年七年级(上)期中数学试卷 题型:解答题
某地区的手机收费标准有两种方式,用户可任性其一:
A.月租费10元,0.1/分,(每次不足1分钟,按一分钟计算)
B.无月租费,0.20元/分,(每次不足1分钟,按一分钟计算)
(1)某用户某月打手机x分钟,则A方式应交付费用为 元;B方式应交付费用为___元;(用含x的代数式表示)
(2)某用户估计一个月内打手机时间为6小时,你认为采用哪种方式更合算?
(1)10+0.1x元;0.20x元;(2)选用A方式合算,理由见解析 【解析】试题分析:(1)应交付费用=月租费+通话费用,把相关数值代入即可求解; (2)6时=360分,把x=360代入(1)得到的式子,求值后比较即可. 试题解析:(1)∵A.月租费10元,0.1/分,某月打手机x分钟, ∴A方式应交付费用:10+0.1x元; B、∵无月租费,0.20元/分,某月...查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌云县2017-2018学年七年级(上)期中数学试卷 题型:填空题
大肠杆菌每20分钟便由一个分裂成2个,经过2小时后,这种大肠杆菌由1个分裂成_____个.
64 【解析】试题解析:∵2小时有6个20分钟, ∴这种大肠杆菌由1个分裂成26=64.查看答案和解析>>
科目:初中数学 来源:黄金30题系列七年级数学 小题好拿分 题型:填空题
如图,下列各图形中的三个数之间均具有相同的规律,依此规律,那么第4个图形中的x= ,一般地,用含有m,n的代数式表示y,即y= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com