
关于x的一元二次方程x2+2x+m=0有两个相等的实数根,则m的值是 .
1 【解析】 试题分析:由已知得△=0,即4-4m=0,解得m=1. 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:单选题
下列说法不一定成立的是( )
A. 若a>b,则a+c>b+c B. 若a+c>b+c,则a>b
C. 若a>b,则ac2>bc2 D. 若ac2>bc2,则a>b
C 【解析】试题解析:选项A、B、D成立,选项C不成立. 故选C.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:填空题
分解因式:1﹣9x2= .
(1+3x)(1﹣3x). 【解析】1﹣9x2=12-(3x)2=(1+3x)(1-3x).查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
(1)y=2x+2(2)15km 【解析】(1)根据函数图象可以得出出租车的起步价是8元,设当x>3时,y与x之间的甬数解析式为y=kx+b(k≠0),运用待定系数法就可以得出结论; (2)将y=32代入(1)中的解析式就可以求出x的值.查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:填空题
如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D是抛物线 y=﹣x2+6x上一点,且在x轴上方,则△BCD 面积的最大值为__________
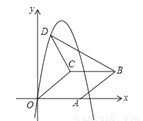
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:单选题
如图,是由几个完全相同的小正方体搭建的几何体,它的左视图是( )
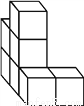
A. 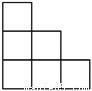 B.
B. 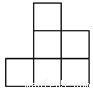 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
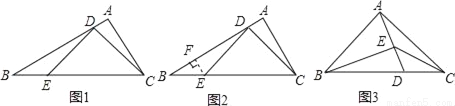
请回答:
(1)小明发现的与CD相等的线段是_____.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求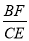 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:单选题
高速铁路列车已成为人们出行的重要交通工具,甲、乙两地相距810km,乘高铁列车从甲地到乙地比乘特快列车少用5h,已知高铁列车的平均速度是特快列车的2.6倍.如果设乘高铁列车从甲地到乙地需y h,那么下面所列方程正确的是( )
A. 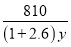 =
=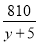 B.
B. 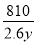 =
=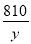 +5 C.
+5 C. 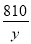 =
= D.
D. 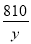 =
=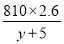
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:解答题
(9分)在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com