
反比例函数y=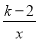 的图象,当x>0时,y随x的增大而减小,则k的取值范围( ).
的图象,当x>0时,y随x的增大而减小,则k的取值范围( ).
A. k<2 B. k≤2 C. k>2 D. k≥2
C 【解析】试题分析:∵反比例函数y=的图象,当x>0时,y随x的增大而减小 ∴k-2>0;解得k>2 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:解答题
先化简,再求值:(1+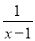 )÷
)÷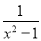 ﹣(x﹣2),其中x=
﹣(x﹣2),其中x=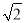 .
.
查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
已知9x2+kxy+4y2是一个完全平方展开式,那么k的值是( )
A. 12 B. 24 C. ±12 D. ±24
C 【解析】已知9x2+kxy+4y2是一个完全平方展开式,中间一项为加上或减去3x和2y积的2倍,所以k=±12.故选C.查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:填空题
不等式组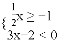 的解集为________.
的解集为________.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:单选题
在△ABC中,∠C=90°,BC=4,sinA=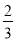 ,那么AC边的长是( )
,那么AC边的长是( )
A. 6 B. 2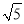 C. 3
C. 3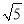 D. 2
D. 2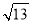
查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
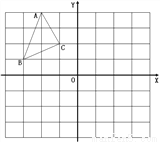
如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(-2,4)、B(-3,1)、C(-1,2)。
(1)在网格内作△A’B’C’,使它与△ABC关于y轴对称。并写出△A’B’C’三个顶点的坐标。
(2)求出四边形ABB’A’的面积。
查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
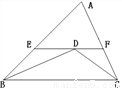
如图,△ABC中,∠ABC与∠ACB的平分线相交于点D,过点D作直线EF‖BC,交AB于点E、交AC于点F若BE=4,EF=7,则FC=____。
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:解答题
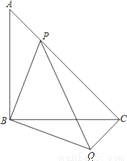
如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:BP=1:3时,求PQ的长;
(3)当点P在线段AC上运动时(P不与A、C重合),请写出一个反映PA2、PC2、PB2之间关系的等式,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
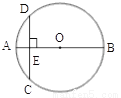
如图,AB是⊙O的直径,CD为⊙O的一条弦,且CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com