
先化简,再求值:(1+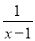 )÷
)÷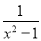 ﹣(x﹣2),其中x=
﹣(x﹣2),其中x=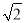 .
.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
若|b-1|+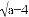 =0,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是________
=0,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是________
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
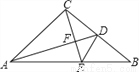
如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
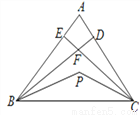
如图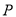 为
为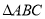 内一点,
内一点, 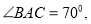
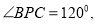
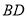 是
是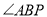 的平分线,
的平分线, 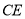 是
是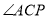 的平分线,
的平分线, 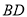 与
与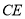 交于
交于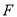 ,则
,则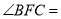 ( )
( )
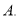
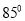
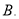
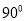
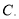
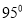
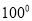
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:解答题
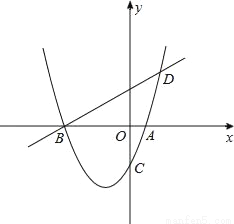
如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=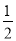 .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:填空题
下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形_____(请填图形下面的代号,答案格式如:“①,②,③,④,⑤”).

查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获利20%,则这种电子产品的标价为( )
A. 26元 B. 27元 C. 28元 D. 29元
C 【解析】试题分析:根据题意,设电子产品的标价为x元,按照等量关系“标价×0.9﹣进价=进价×20%”,列出一元一次方程得:0.9x﹣21=21×20%解得:x=28所以这种电子产品的标价为28元. 故选C.查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
用反证法证明AB≠AC时,首先假设________成立.
AB=AC 【解析】反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立. 由此可得用反证法证明AB≠AC时,首先假设AB=AC成立.查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:单选题
反比例函数y=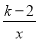 的图象,当x>0时,y随x的增大而减小,则k的取值范围( ).
的图象,当x>0时,y随x的增大而减小,则k的取值范围( ).
A. k<2 B. k≤2 C. k>2 D. k≥2
C 【解析】试题分析:∵反比例函数y=的图象,当x>0时,y随x的增大而减小 ∴k-2>0;解得k>2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com