练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点P(3，2)关于原点对称的点在( )

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    C 【解析】试题分析：关于原点对称后，点的横纵坐标都变为相反数，则点P关于原点对称后的点的坐标为(-3，-2)，则点在第三象限，故选择C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

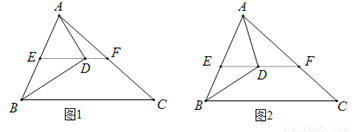
    如图，在△ABC中，点D为∠ABC的平分线BD上一点，连接AD，过点D作EF∥BC交AB于点E，交AC于点F．

    （1）如图1，若AD⊥BD于点D，∠BEF=130°，求∠BAD的度数；

    （2）如图2，若∠ABC=α，∠BDA=β，求∠FAD+∠C的度数（用含α和β的代数式表示）．

    （1）65°；（2）∠FAD+∠C=β﹣α． 【解析】试题分析：(1)利用角平分线可得是等腰三角形，可以得到∠ABD的度数，AD⊥BD,所以可以得到∠BAD的度数. (2)利用（1）的方法，可求得∠FAD+∠C的度数. 试题解析： 【解析】 （1）∵EF∥BC，∠BEF=130°， ∴∠EBC=50°，∠AEF=50°， 又∵BD平分∠EBC， ∴∠EB...

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期6.1数据的收集 同步练习 题型：填空题

    进行数据的收集调查时，在明确调查问题、确定调查对象后，还要完成以下4个步骤：①展开调查 ②得出结论 ③记录结果 ④选择调查方法，但它们的顺序弄乱了，正确的顺序应该是_____（填写序号即可）．

    ④①③②． 【解析】进行数据的调查收集，一般可分为以下4个步骤：④选择调查方法；①展开调查；③记录结果；②得出结论， 故答案为：④①③②．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型：解答题

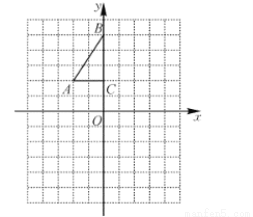
    如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).

    (1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.

    (2)平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形.

    (3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标.

    (1)作图见解析；（2）作图见解析；（3）(0，-2). 【解析】试题分析：（1）利用旋转的性质得出对应点坐标进而得出答案； （2）利用平移规律得出对应点位置，进而得出答案； （3）利用旋转图形的性质，连接对应点，即可得出旋转中心的坐标． 试题解析：（1）如图所示：△A1B1C即为所求； （2）如图所示：△A2B2C2即为所求； （3）旋转中心坐标（0，﹣2）．...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型：填空题

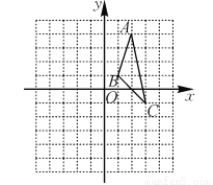
    如图，在平面直角坐标系中，△ABC与△A1B1C1关于原点对称，则点A1、B1、C1的坐标分别为____

    (-2，-4)，(-1，-1)，(-3，1). 【解析】试题分析：关于原点对称后，点的横纵坐标都变为相反数，根据题意可得：A(2,4)、B(1,1)、C(3，-1)，则关于原点对称后的点坐标分别为： ．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：解答题

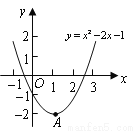
    如图，已知二次函数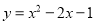的图象的顶点为A．二次函数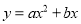的图象与x轴交于原点O及另一点C，它的顶点B在函数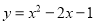的图象的对称轴上．

    （1）求点A与点C的坐标；

    （2）当四边形AOBC为菱形时，求函数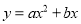的关系式．

    （1）C（2，0）；（2）. 【解析】试题分析：（1）二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上，可知两个函数对称轴相等，因此先根据已知函数求出对称轴．根据函数解析式得出顶点A的坐标与对称轴，故可得出二次函数y=ax2+bx关于x=1对称，且函数与x轴的交点分别是原点和C点，所以点C和点O关于直线l对称，故可得出点C的坐标； （2）因为四边形AOBC是菱形，根据菱形性...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：填空题

    已知二次函数y=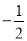x2-7x+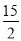，若自变量x分别取x1，x2，x3，且0＜x1＜x2＜x3，则对应的函数值y1，y2，y3的大小关系是__________________（用“<”连接）。

    y3

    查看答案和解析>>

    科目：初中数学 来源：2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型：解答题

    如图，已知△ACE，△ABF都是等腰直角三角形，且∠BAF＝∠CAE＝90°.那么你能利用旋转的知识说明FC＝BE吗？

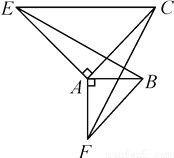
    理由见解析. 【解析】试题分析：由AE，AB绕A点顺时针旋转90°分别与AC，AF重合，得到△AFC可看作是△ABE绕A点顺时针旋转90°得到的，从而得到结论． 试题解析：【解析】 ∵AE，AB绕A点顺时针旋转90°分别与AC，AF重合，∴△AFC可看作是△ABE绕A点顺时针旋转90°得到的，∴FC＝BE．

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    若点P（x，5）在第二象限内，则x应是（ ）

    A. 正数 B. 负数 C. 非负数 D. 有理数

    B 【解析】在第二象限时，横坐标＜0，纵坐标＞0，因而就可得到x＜0，即可得解． 【解析】 ∵点P（x，5）在第二象限， ∴x＜0，即x为负数． 故选B． “点睛”解决本题解决的关键是熟记在各象限内点的坐标的符号，第一象限点的坐标符号为（+，+），第二象限点的坐标符号为（-，+），第三象限点的坐标符号为（-，-），第四象限点的坐标符号为（+，-）．

    查看答案和解析>>

    同步练习册答案