练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

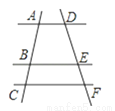
    如图，直线AD∥BE∥CF，BC=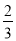AB，DE=6，那么EF的值是________ ．

    4． 【解析】∵AD∥BE∥CF，BC＝AB， ∴＝=， 即=， 解得EF=4. 故答案为4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省金华市2017-2018学年七年级上册期末模拟数学试卷 题型：单选题

    如图，数轴上A点表示的数减去B点表示的数，结果是（ ）

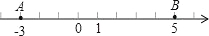
    A. 8 B. -8 C. 2 D. -2

    B 【解析】【解析】 由图可知：A表示-3，B表示5，故数轴上点A表示的数减去点B表示的数，结果是-3-5=-8．故选B．

    查看答案和解析>>

    科目：初中数学 来源：重庆市长寿区2017-2018学年七年级（上）期中数学 题型：填空题

    若单项式ax2yn+1与axmy4的差仍是单项式，则m﹣2n=_____．

    -4 【解析】∵单项式与的差仍是单项式， ∴单项式与是同类项， ∴ ，解得： ， ∴.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2018届九年级上册期末模拟数学试卷 题型：解答题

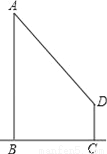
    如图，一位同学想利用树影测量树高（AB），他在某一时刻测得高为1m的竹竿影长为0.9m，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上（CD），他先测得留在墙上的影高（CD）为1.2m，又测得地面部分的影长（BC）为2.7m，他测得的树高应为多少米？

    测得的树高为4.2米． 【解析】先求出墙上的影高CD落在地面上时的长度，再设树高为h，根据同一时刻物高与影长成正比列出关系式求出h的值即可

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2018届九年级上册期末模拟数学试卷 题型：填空题

    用长度一定的绳子围成一个矩形，如果矩形的一边长x(m)与面积y(m2)满足函数关系y＝－(x－12)2＋144(0＜x＜24)，那么该矩形面积的最大值为________m2 ．

    144 【解析】∵且， ∴当时，最大=. 即：该矩形面积的最大值为m2.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2018届九年级上册期末模拟数学试卷 题型：单选题

    如图，直线l⊥x轴于点P，且与反比例函数y1=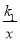（x＞0）及y2=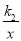（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2的值为（　　）

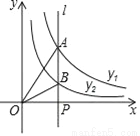
    A. 2 B. 3 C. 4 D. ﹣4

    C 【解析】试题解析：根据反比例函数k的几何意义可知：△AOP的面积为，△BOP的面积为， ∴△AOB的面积为-， ∴-=2， ∴k1﹣k2=4， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（六） 题型：解答题

    夏季来临，商场准备购进甲、乙两种空调，已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同．请解答下列问题：

    （1）求甲、乙两种空调每台的进价；

    （2）若甲种空调每台售价2500元，乙种空调每台售价1800元，商场计划用不超过36000元购进空调共20台，且全部售出，请写出所获利润y（元）与甲种空调x（台）之间的函数关系式，并求出所能获得的最大

    利润.

    （1）甲种空调每台2000元，乙种空调每台1500元； （2）所获利润y（元）与甲种空调x（台）之间的函数关系式是y=200x+6000，所获的最大利润是8400元． 【解析】试题分析：（1）根据题意可以列出相应的方程，从而可以分别求得甲、乙两种空调每台的进价，注意分式方程要检验；（2）根据题意和（1）中的答案可以得到所获利润y（元）与甲种空调x（台）之间的函数关系式，然后根据商场计划...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省沧州市中考数学模拟试卷（六） 题型：单选题

    反比例函数y=（k＞0）的部分图象如图所示，A，B是图象上两点，AC⊥x轴于点C，BD⊥x轴于点D，若△AOC的面积为S1，△BOD的面积为S2，则S1和S2的大小关系为（　　）

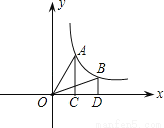
    A. S1＞S2 B. S1=S2 C. S1＜S2 D. 无法确定

    B 【解析】试题解析：依据比例系数k的几何意义可得两个三角形的面积都等于 故 故选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级12月月考数学试卷 题型：解答题

    计算： ．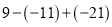

    -1 【解析】试题分析：本题考查了有理数的加减混合运算，计算时先根据减法法则把减法转化为加法，然后再按照加法法则计算即可. 原式＝ ＝ ＝．

    查看答案和解析>>

    同步练习册答案