
��ͼ���ڡ�ABC�У�AB=AC����A=36�㣬DE��AC�Ĵ�ֱƽ���ߣ�
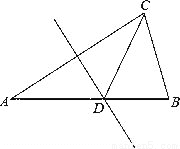
��1����֤����BCD�ǵ��������Σ�
��2����BCD���ܳ���a��BC=b�����ACD���ܳ����ú�a��b�Ĵ���ʽ��ʾ��
��1������������2��a��b+b+b=a+b�� ���������������:��1������AB=AC����A=36�㣬�����B=��ACB==72�㣬Ȼ����DE��AC�Ĵ�ֱƽ���ߣ��ɵ�AD=DC�������ɵá�ACD=��A=36�㣬Ȼ�������ǵ����ʿ���CDB=��ACD+��A=72�㣬���ݵȽǶԵȱ߿ɵã�CD=CB��������֤��BCD�ǵ��������Σ� ��2���ɣ�1��֪��AD=CD=CB=b���ɡ�BCD���ܳ���...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭���ݹ�������������2017-2018ѧ�����꼶��ѧ��������ѧ ���ͣ���ѡ��
����˵����ȷ���۵�����ǣ� ����
��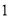 ��
��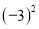 ������ƽ������
������ƽ������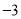 �� ��
�� ��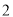 ��
��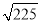 ƽ������
ƽ������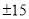 ��
��
��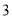 ����
����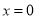 ��
��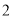 ʱ��
ʱ�� 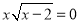 �� ��
�� ��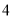 ��
��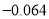 ����������
����������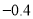 ��
��
A. ��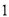 ����
����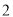 ����
����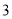 ����
����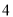 �� B. ��
�� B. ��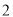 ����
����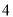 ��
��
C. ��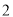 ����
����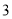 ����
����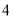 �� D. ��
�� D. ��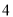 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2016-2017���꼶��ѧ������ĩ�Ծ� ���ͣ������
��8�֣� ��ͼ����C��M��N������DQ�ϣ���B������AP�ϣ���AP��DQ����D=��ABC=80�㣬��1=��2��ANƽ�֡�DAM��
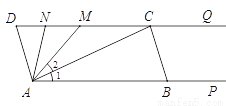
��1����˵��AD��BC�����ɣ�
��2�������CAN�Ķ�����
��3��ƽ���߶�BC��
�����ʡ�AMD����ACD��ֵ�Ƿ����仯�������ᣬ����������ֵ�����ᣬ���ҳ���Ӧ�仯���ɣ�
������ƽ�ƹ����д���ij��λ�ã�ʹ�á�AND=��ACB�������ʱ��ACB�Ķ�����
��1��������;(2) ��CAN��50��;(3)�ٲ���, ��AMD����ACD��2;�ڡ�ACB��75�㣮 �������������������1����ƽ���ߵ����ʺ��ж����ɵõ����ۣ� ��2���ɽ�ƽ���ߵĶ���ͽǵĺͲ���Եõ����ۣ� ��3���ٲ��ᣮ����ƽ���ߵ����ʼ��ɵõ����ۣ� ����ƽ���ߵ����ʺ͡�AND����ACB���õ���NAB����DAC�������õ���1����DAN�����ɵõ����ۣ� �����������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2016-2017���꼶��ѧ������ĩ�Ծ� ���ͣ���ѡ��
��֪a��bΪ��������ab��0����M=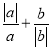 ����a��bȡ��ͬ��ֵʱ��M��ֵ��( )
����a��bȡ��ͬ��ֵʱ��M��ֵ��( )
A. ��2 B. ��1���2 C. 0���1 D. 0���2
D ���������������� ������������ۣ��ٵ�a��0��b��0ʱ��M=1+1=2�� �ڵ�a��0��b��0ʱ��M=��1+����1��=��2�� ��a��0��b��0ʱ��M=1��1=0�� �ܵ�a��0��b��0ʱ��M=��1+1=0�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2016-2017���꼶��ѧ������ĩ�Ծ� ���ͣ���ѡ��
��ͼ�У���������չ��ͼ����( )
A. 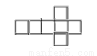 B.
B. 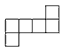 C.
C. 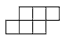 D.
D. 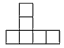
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����й�����2017��2018ѧ���һѧ�ڰ��꼶��ѧ��ĩ�����Ծ� ���ͣ������
���㣺
��1������a2��3•4a ��2��2x��x+1��+��x+1��2��
(1)-4a7; (2) 3x2+4x+1�� ���������������:��1�������ݵij˷���ͬ�����ݵij˷����м��㼴�ɣ� ��2�����ݵ���ʽ���Զ���ʽ�Լ���ȫƽ����ʽ���м��㼴�ɣ� �������� ��1��ԭʽ=��a6•4a =��4a7�� ��2��ԭʽ=2x2+2x+x2+2x+1 =3x2+4x+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����й�����2017��2018ѧ���һѧ�ڰ��꼶��ѧ��ĩ�����Ծ� ���ͣ���ѡ��
��ͼ����֪��MON=30�㣬��A1��A2��A3����������ON�ϣ���B1��B2��B3����������OM�ϣ���A1B1A2����A2B2A3����A3B3A4������Ϊ�ȱ������Σ���OA1=2�����A5B5A6�ı߳�Ϊ( )
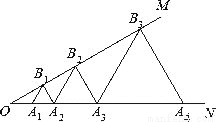
A. 8 B. 16 C. 24 D. 32
B ����������ͼ��ʾ�� �ߡ�A1B1A2�ǵȱ������Σ� ��A1B1=A2B1����3=��4=��12=60�㣬 ���2=120�㣬 �ߡ�MON=30�㣬 ���1=180�㩁120�㩁30��=30�㣬 �֡ߡ�3=60�㣬 ���5=180�㩁60�㩁30��=90�㣬 �ߡ�MON=��1=30�㣬 ��OA1=A1B1=1�� ��A2B1=1�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰����꼶��ѧ�²���ϰ���ڰ��´����� ���ͣ������
�ⷽ����
��1��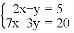
��2��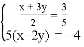
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018���Ϻ��з������п���ѧһģ�Ծ� ���ͣ������
��֪����ͼ��������ABCD�У�AB��CD����D=90�㣬AD=CD=2����E�ڱ�AD�ϣ������A��D�غϣ�����CEB=45�㣬EB��Խ���AC�ཻ�ڵ�F����DE=x��
��1���ú�x�Ĵ���ʽ��ʾ�߶�CF�ij���
��2������ѡ�CAE���ܳ�����C��CAE����BAF���ܳ�����C��BAF����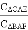 =y����y����x�ĺ�����ϵʽ����д�����Ķ�����
=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3������ABE������ֵ�� ʱ����AB�ij���
ʱ����AB�ij���
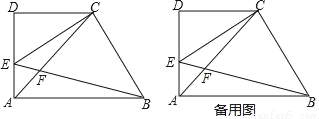
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com