
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
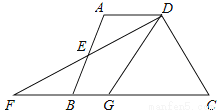
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
证明见解析;(2)GE垂直平分DF. 【解析】 试题分析:(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE; (2)∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE...科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:解答题
已知:三角形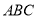 .
.
( )比较线段
)比较线段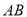 ,
, 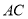 ,
, 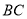 的大小,并用
的大小,并用 号连结.
号连结.
( )用直尺和圆规在直线
)用直尺和圆规在直线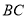 上,作点
上,作点 ,使
,使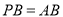 ,不写作法,保留作图痕迹.
,不写作法,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:单选题
在△ABC中,作BC边上的高,以下作图正确的是( )
A. 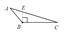 B.
B. 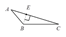 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型:填空题
一个三角形的两边分别是5cm和3cm,则第三边xcm的取值范围是_______________
2<x<8 【解析】试题分析:根据三角形的三边关系三角形两边之和大于第三边.三角形的两边差小于第三边可得5-3<x<5+3,再解即可. 试题解析:根据三角形的三边关系可得:5-3<x<5+3, 即:2<x<8.查看答案和解析>>
科目:初中数学 来源:浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型:单选题
已知:直角三角形的两条直角边的长分别为3和4,则第三边长为( )
A. 5 B. 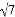 C.
C. 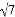 或5 D.
或5 D. 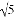
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:填空题
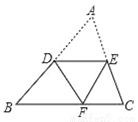
如图,△ABC中,点D、E分别在边AB、AC的中点,将△ADE沿过DE折叠,使点A落在BC上F处,若∠B=50°,则∠BDF=______度.
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
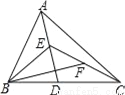
如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
A. 2 cm2 B. 1 cm2 C. 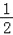 cm2 D.
cm2 D. 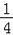 cm2
cm2
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
先化简再求值: 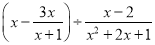 ,其中
,其中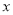 满足
满足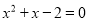 .
.
查看答案和解析>>
科目:初中数学 来源:辽宁省鞍山市铁西区2017-2018学年七年级(上)期中数学试卷 题型:单选题
有下列各式:m,﹣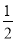 ,x﹣2,
,x﹣2, 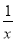 ,
, 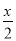 ,﹣
,﹣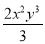 ,
, 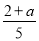 ,其中单项式有( )
,其中单项式有( )
A. 5个 B. 4个 C. 3个 D. 2个
B 【解析】∵m,﹣ , ,﹣是单项式; x﹣2, 是多项式; 是分式; ∴单项式有4个. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com