练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知y是x﹣3的正比例函数，且当x=2时，y=﹣3．

    （1）求y与x之间的函数关系式；

    （2）求当x=1时，y的值；

    （3）求当y=﹣12时，x的值．

    （1）；（2）；（3） 【解析】试题分析：（1）根据y与x-3成正比例，设出一次函数的关系式，再把当x=2时，y=-3代入求出k的值即可； （2））把x=1代入y=3x-9即可求得y的值； （3）把y=-12代入y=3x-9即可求得x的值． 试题解析：（1）∵y与x-3成正比例，设出一次函数的关系式为：y=k（x-3）（k≠0）， 把当x=2时，y=-3代入得：-3=...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    下列说法:①等边三角形是等腰三角形;②等腰三角形也可能是直角三角形;③三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】∵①“等边三角形是等腰三角形”的说法正确；②“等腰三角形也可能是直角三角形”的说法正确；③“三角形按边分为等腰三角形、等边三角形和三边都不相等的三角形”的说法是错误的（因为等边三角形属于等腰三角形）；④“三角形按角分类应分为锐角三角形、直角三角形和钝角三角形”是正确的； ∴上述说法中正确的有3种. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：解答题

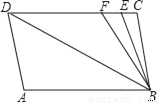
    如图，已知直线AB∥CD，∠A=∠C=100°，E，F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．

    （1）求证：AD∥BC；

    （2）求∠DBE的度数；

    （3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出其度数；若不存在，请说明理由．

    （1）证明见解析；（2）40°；（3）60°. 【解析】试题分析：（1）根据平行线的性质，以及等量代换证明∠ADC+∠C=180°，即可证得AD∥BC； （2）由直线AB∥CD，根据两直线平行，同旁内角互补，即可求得∠ABC的度数，又由∠DBE=∠ABC，即可求得∠DBE的度数． （3）首先设∠ABD=∠DBF=∠BDC=x°，由直线AB∥CD，根据两直线平行，同旁内角互补与两直...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：单选题

    如图，直线a∥b，∠1 = 60°，∠2 = 40°，则∠3等于（ ）

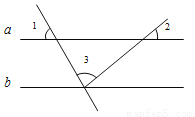
    A. 40° B. 60° C. 80° D. 100°．

    C 【解析】试题分析：根据平行线的性质：两直线平行，同位角相等，可知∠1=∠5=60°，∠2=∠4=40°，可求然后根据平角的定义可求∠3=180°-60°-40°=80°． 故选C

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，△ABC中，∠ABC与∠ACB的角平分线相交于点D，过D点的直线EF∥BC且交AB于E、交AC于F，已知AB=7cm，AC=5cm，BC=6cm，则△AEF的周长为_____cm．

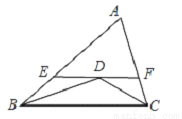
    12 【解析】试题解析：∵BD是角平分线， ∴∠ABD=∠CBD， ∵FE∥BC， ∴∠DBC=∠DBE， ∴∠DBE=∠EDB， ∴BE=ED， 同理DF=DC， ∴△AED的周长=AE+AF+EF=AB+AC=5+7=12（cm） 故答案为：12．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    计算： =________．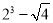

    6 【解析】试题解析： =8-2=6. 故答案为：6.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型：单选题

    如图，在△ABC中，AB＝AC，∠ABC＝75°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为( )

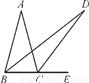
    A. 15° B. 17.5° C. 20° D. 22.5°

    A 【解析】因为AB＝AC，∠ABC＝75°，所以∠A=30°. 因为∠ABC与∠ACE的平分线相交于点D，所以∠ABD=∠EBD，∠ACD=∠ECD. 设ABD=∠EBD=x，∠ACD=∠ECD=y，则 2y=2x+30°①， y=x+∠D ② 联立①②得，∠D=15°. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型：单选题

    如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有(　　)

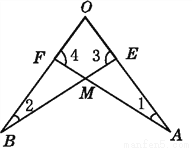
    A. 1对 B. 2对 C. 3对 D. 4对

    B 【解析】【解析】 ∵∠3=∠4，OE=OF，又∠O=∠O，∴△AOF≌△BOE． ∵△AOF≌△BOE，∴OA=OB．又∵OE=OF，∴AE=BF．∵∠1=∠2，∠AME=∠BMF，AE=BF，∴△AEM≌△BFM． 共2对．故选B．

    查看答案和解析>>

    同步练习册答案