练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

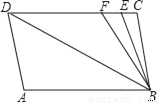
    如图，已知直线AB∥CD，∠A=∠C=100°，E，F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．

    （1）求证：AD∥BC；

    （2）求∠DBE的度数；

    （3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出其度数；若不存在，请说明理由．

    （1）证明见解析；（2）40°；（3）60°. 【解析】试题分析：（1）根据平行线的性质，以及等量代换证明∠ADC+∠C=180°，即可证得AD∥BC； （2）由直线AB∥CD，根据两直线平行，同旁内角互补，即可求得∠ABC的度数，又由∠DBE=∠ABC，即可求得∠DBE的度数． （3）首先设∠ABD=∠DBF=∠BDC=x°，由直线AB∥CD，根据两直线平行，同旁内角互补与两直...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    数学课上,老师出了一道题:化简

    [8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].

    小明同学马上举手,下面是小明的解题过程:

    [8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]

    =[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3

    =(a+b)2-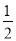 (a+b)+ .

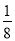    小亮也举起了手,说小明的解题过程不对,并指了出来.老师肯定了小亮的回答.你知道小明错在哪儿吗?请指出来,并写出正确解答.

    第一处错是(-a-b)3=(a+b)3;第二处错是2(a+b)3=8(a+b)3. 【解析】试题分析：分析题意，根据负数的奇数次幂的性质可以确定第一步中化简(-a-b)3时是错误的，将a+b看成一个整体，由乘方的意义知第二步中计算除数是8(a+b)3不对，而是等于2(a+b)3. 解:第一处错是(-a-b)3=(a+b)3;第二处错是2(a+b)3=8(a+b)3.正确解答如下: ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：单选题

    不一定在三角形内部的线段是( )

    A. 三角形的角平分线 B. 三角形的中线

    C. 三角形的高 D. 以上都不对

    C 【解析】试题解析：三角形的角平分线、中线一定在三角形的内部， 直角三角形的高线有两条是三角形的直角边， 钝角三角形的高线有两条在三角形的外部， 所以，不一定在三角形内部的线段是三角形的高. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：解答题

    如图，把一个三角板（AB=BC，∠ABC=90°）放入一个“U”形槽中，使三角板的三个顶点A、C、B分别在槽的两壁及底边上滑动，已知∠D=∠E=90°，在滑动过程中，你发现线段AD与BE有什么大小关系？试说明你的结论.

    ，见解析 【解析】【解析】 易发现AD与BE所在的△ABD与△BCE在滑动过程中始终全等，因而AD=BE．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：填空题

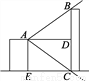
    如图，某人在楼顶A点处看到一烟囱顶端B的仰角∠BAD＝42°，看到烟囱底部C的俯角∠CAD也是42°，如果楼AE高是15米，那么烟囱BC高__米．

    30 【解析】∵∠BAD=∠CAD=42°， ∴AD是∠BAC的平分线. ∵AD⊥BC， ∴BD=CD. ∴BC=2CD=2AE=30. 故烟囱的高度为30米.故答案为:30.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：填空题

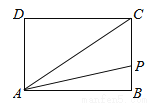
    如图，长方形ABCD中，AB=5，AD=3，点P从点A出发，沿长方形ABCD的边逆时针运动，设点P运动的距离为x；△APC的面积为y，如果5<x<8，那么y关于x的函数关系式为__________．

    y=–x+20 【解析】试题解析：当5＜x＜8时，点P在线段BC上，PC=8﹣x， ∴y=PC•AB=﹣x+20． 故答案为：y=﹣x+20．

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：单选题

    甲、乙两人以相同路线前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：

    ①乙比甲提前12分钟到达；

    ②甲的平均速度为15千米/小时；

    ③乙走了8km后遇到甲；

    ④乙出发6分钟后追上甲．

    其中正确的有（ ）

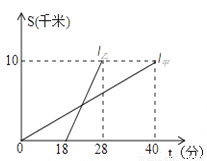
    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】试题分析：此题考查的是读函数的图象，首先要理解横纵坐标表示的含义，函数的横坐标表示时间，纵坐标表示路程，理解问题叙述的过程，能够通过图象知道函数是随自变量的增大而增大，然后根据图象上特殊点的意义进行解答: ①乙在28分时到达，甲在40分时到达，所以乙比甲提前了12分钟到达；故①正确； ②根据甲到达目的地时的路程和时间知：甲的平均速度=10÷4060=15千米/时； ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    已知y是x﹣3的正比例函数，且当x=2时，y=﹣3．

    （1）求y与x之间的函数关系式；

    （2）求当x=1时，y的值；

    （3）求当y=﹣12时，x的值．

    （1）；（2）；（3） 【解析】试题分析：（1）根据y与x-3成正比例，设出一次函数的关系式，再把当x=2时，y=-3代入求出k的值即可； （2））把x=1代入y=3x-9即可求得y的值； （3）把y=-12代入y=3x-9即可求得x的值． 试题解析：（1）∵y与x-3成正比例，设出一次函数的关系式为：y=k（x-3）（k≠0）， 把当x=2时，y=-3代入得：-3=...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018 北师大版七年级数学下册 第三章　变量之间的关系 单元测试卷 题型：解答题

    某机动车出发前油箱内有油42L.行驶若干小时后，途中在加油站加油若干升．油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示，根据图象回答问题．

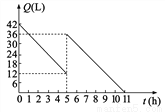
    (1)机动车行驶几小时后加油？

    (2)中途加油________L；

    (3)如果加油站距目的地还有240km，车速为40km/h，要到达目的地，油箱中的油是否够用？并说明原因．

    (1)5小时(2)24(3)油箱中的油刚好够用． 【解析】试题分析：（1）根据图象可得，5小时时，机动车内的油从12升变为了36升，故5小时后加油； （2）用36-12即可； （3）首先计算出耗油量，再根据路程和速度计算出行驶240km的时间，然后用时间乘以耗油量可得所消耗的油，和油箱里的油量进行比较即可． 试题解析：(1)根据图象可直接得到：机动车行驶5小时后加油； ...

    查看答案和解析>>

    同步练习册答案