练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC= 　. 

    知识点五:线段的性质

    6cm 【解析】因为点D是线段AC的中点，所以AC=2DC.因为CB=4cm，DB=7 cm，所以CD=BD－BC=3cm，所以AC=6 cm.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级上册 第三章 整式及其加减 3．3　整式 同步测试卷 含答案 题型：单选题

    下列说法错误的是（　　）

    A. 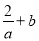是一次二项式

    B. x6－1是六次二项式

    C. 3x4－5x2y2－6y3＋2是四次四项式

    D. 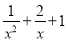不是多项式

    A 【解析】A.选项是分式，不是一次二项式，故错误； B. 是六次二项式，故正确； C：3x4－5x2y2－6y3＋2是四次四项式，故正确； ∵D选项是四次三项式，与选项中一致， ∴D不是多项式，故正确. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型：单选题

    二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x=2，下列结论：

    ①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞﹣1时，y的值随x值的增大而增大．

    其中正确的结论有（ ）

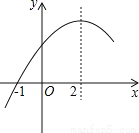
    A．1个 B．2个 C．3个 D．4个

    B 【解析】 试题分析：根据抛物线的对称轴为直线x=﹣=2，则有4a+b=0；观察函数图象得到当x=﹣3时，函数值小于0，则9a﹣3b+c＜0，即9a+c＜3b；由于x=﹣1时，y=0，则a﹣b+c=0，易得c=﹣5a，所以8a+7b+2c=8a﹣28a﹣10a=﹣30a，再根据抛物线开口向下得a＜0，于是有8a+7b+2c＞0；由于对称轴为直线x=2，根据二次函数的性质得到当x＞2时...

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.3角同步练习 题型：填空题

    用度、分、秒表示91.34°为________.

    【解析】试题分析：因为0．34°=0．34×60′=20．4′，而0．4′=0．4×60″=24″，所以91．34°=91°20′24″．

    查看答案和解析>>

    科目：初中数学 来源：福建省漳州市北师大版七年级数学上册校本作业：4.2比较线段的长短 题型：解答题

    在下图中，C，D是线段AB上的两点，已知BC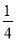＝AB，AD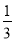＝AB，AB＝12 cm，求CD，BD的长．

    CD＝5cm，BD＝8cm． 【解析】试题分析：首先根据AB、BC和AD的关系求出BC和AD的长度，然后根据CD=AB-AD-BC以及BD=DC+BC求出线段的长度． 试题解析：∵AB=12cm， ∴BC=AB=×12=3cm，AD=AB=×12=4cm， ∴CD=AB-AD-BC=12-4-3=5cm，BD=DC+BC=5+3=8cm． 试题分析：本题主要考查的就是线段长...

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.1线段、直线、射线 同步练习 题型：解答题

    已知四点A、B、C、D，按照下列语句画出图形；

    （1）作线段AD，并以cm为单位，度量其长度；

    （2）线段AC和线段DB相交于点O；

    （3）反向延长线段BC至E，使BE=BC．

    图形见解析 【解析】试题分析:(1)根据线段的定义,连接AD,即可得线段AD,然后用直尺量出AD的长度即可,(2)根据线段的定义和题目要求,连接AC和BD,两线段的交点即为点O,(3)根据反向延长线的定义,沿CB方向延长,使得BE的长度等于BC即可. 试题解析:如图所示,AD=3.5cm,

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.1线段、直线、射线 同步练习 题型：填空题

    如图，图中有__条直线，有__条射线，有__条线段，以E为顶点的角有__个．

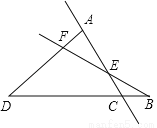
    1 9 12 4 【解析】如图,图中有直线AC,共1条直线,有A为端点的2条射线,B为端点的1条射线,C为端点的2条射线,E为端点的3条射线,F为端点的1条射线,共9条射线,有线段AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,DF,EF,共12条线段,以E为顶点的角有∠AEB,∠AEF, ∠BEC,∠CEF,共4个,故答案为:1,9,12,4.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.2中心对称图形 测试 题型：单选题

    下列标志图中，既是轴对称图形，又是中心对称图形的是（　）

    A. B. C. D.

    B 【解析】试题解析：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故A选项错误； B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故B选项正确； C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故C选项错误； D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对...

    查看答案和解析>>

    科目：初中数学 来源：山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    （本题共10分）AB和AC 相交于点A， BD和CD相交于点D，探究∠BDC与∠B 、 ∠C、∠BAC的关系．

    小明是这样做的：

    解：以点A为端点作射线AD．

    ∵∠1是△ABD的外角，∴∠1= ∠B+∠BAD．

    同理∠2=∠C+∠CAD．

    ∴∠1+∠2=∠B+∠BAD+∠C+∠CAD．即∠BDC=∠B+∠C+∠BAC．

    小英的思路是：延长BD交AC于点E．

    （1）按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论．

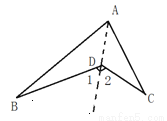
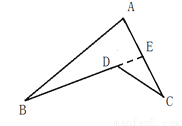
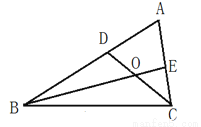
    （2）按照上面的思路解决如下问题：如图：在△ABC中，BE、CD分别是∠ABC∠ACB的角平分线，交AC于E，交AB于D．BE、CD相交于点O，∠A=60°．求∠BOC的度数．

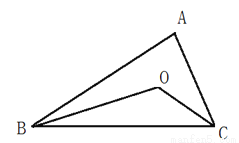
    （3）如图：△ABC中，BO、CO分别是∠ABC与∠ACB的角平分线，且BO、CO相交于点O．猜想∠BOC与∠A有怎样的关系，并加以证明．

    （1）证明见解析；（2）120°；（3）∠BOC=90°+ ∠A． 【解析】试题分析： （1）按小英的思路：∠BDC是△DCE的外角，∠DEC是△ABE的外角，则由三角形外角的性质可得；∠BDC=∠C+∠DEC，∠DEC=∠B+∠BAC，由此可得：∠BDC=∠C+∠B+∠BAC； （2）由△ABC中，BE、CD分别是∠ABC∠ACB的角平分线，交AC于E，交AB于D．BE、CD相...

    查看答案和解析>>

    同步练习册答案