
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
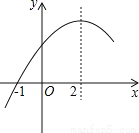
A.1个 B.2个 C.3个 D.4个
B 【解析】 试题分析:根据抛物线的对称轴为直线x=﹣=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时...科目:初中数学 来源:北师大版七年级上册 第五章 一元一次方程 5.1 认识一元一次方程 同步测试卷 含答案 题型:填空题
若关于x的方程2x-(2a-1)x+3=0的解是x=3,则a=( )
A. 0 B. 1 C. 2 D. 3
C 【解析】根据方程解的定义将x=3代入方程可得: ,解方程可得: a=2,故选C.查看答案和解析>>
科目:初中数学 来源:人教版数学七年级下册(贵州专版) 期中综合检测 题型:解答题
如图所示,用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B.则走哪条路吃到的胡萝卜最多?走哪条路吃到的青菜最多?
(1)点C的坐标是(2,1),它表示的意义是放置2个胡萝卜、1棵青菜;点D的坐标是(2,2),它表示的意义是放置2个胡萝卜、2棵青菜;点E的坐标是(3,3),它表示的意义是放置3个胡萝卜、3棵青菜;点F的坐标是(3,2),它表示的意义是放置3个胡萝卜、2棵青菜. (2)走第③条路吃到的胡萝卜、青菜都最多,理由见解析. 【解析】试题分析: 由点A的坐标(3,1),点B的坐标(2,3)可以...查看答案和解析>>
科目:初中数学 来源:人教版数学七年级下册(贵州专版) 期中综合检测 题型:单选题
如图所示,AB∥CD,BC平分∠ABD,若∠C=40°,则∠D的度数为 ( )

A. 90° B. 100° C. 110° D. 120°
B 【解析】∵AB//CD,∠C=40°, ∴∠ABC=∠C=40°, ∵BC平分∠ABD, ∴∠DBC=∠ABC=40°, ∴∠D=180°-∠C-∠DBC=180°-40°-40°=100°. 故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)和正比例函数y=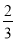 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣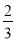 )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )
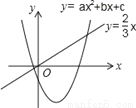
A. 大于0 B. 等于0 C. 小于0 D. 不能确定
A 【解析】试题分析:设ax2+bx+c=0(a≠0)的两根为x1,x2,由二次函数的图象可知x1+x2>0,a>0,设方程ax2+(b﹣)x+c=0(a≠0)的两根为a,b再根据根与系数的关系即可得出结论. 设ax2+bx+c=0(a≠0)的两根为x1,x2, ∵由二次函数的图象可知x1+x2>0,a>0, ∴﹣>0. 设方程ax2+(b﹣)x+c=0(a≠0)的两根为a,b,...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.2二次函数与一元二次方程 练习 题型:单选题
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a-2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A. ①② B. ①④ C. ①③④ D. ②③④
B 【解析】试题分析:根据抛物线与x轴有两个交点可得b2﹣4ac>0,进而判断①正确; 根据题中条件不能得出x=﹣2时y的正负,因而不能得出②正确; 如果设ax2+bx+c=0的两根为α、β(α<β),那么根据图象可知不等式ax2+bx+c>0的解集是x<α或x>β,由此判断③错误; 先根据抛物线的对称性可知x=﹣2与x=4时的函数值相等,再根据二次函数的增减性即可判断④正...查看答案和解析>>
科目:初中数学 来源:初一数学第一学期4.3角同步练习 题型:填空题
在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
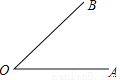
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB
小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.
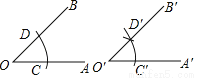
老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
SSS(三角形全等或全等三角形的对应角相等) 【解析】试题分析:根据作图的方法可知:OD=OD′,OC=OC′,CD=C′D′,则根据SSS来判定三角形全等,即可得出∠AOB=∠A′OB′.查看答案和解析>>
科目:初中数学 来源:福建省漳州市北师大版七年级数学上册校本作业:4.2比较线段的长短 题型:填空题
如图,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC= .

知识点五:线段的性质
6cm 【解析】因为点D是线段AC的中点,所以AC=2DC.因为CB=4cm,DB=7 cm,所以CD=BD-BC=3cm,所以AC=6 cm.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题(含答案) 题型:填空题
写出下列图中x的值:
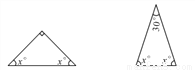
(1)x=______.(2)x=______.
45 75 【解析】(1)∵2x°+90°=180°,∴x=45. (2)∵2x°+30°=180°,∴x=75. 故答案为:(1)45;(2)75.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com