练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图，在△ABC中，D是BC边上的一点，连接AD，取AD的中点E，过点A作BC的平行线与CE的延长线交于点F，连接DF．

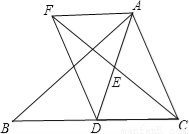
    （1）求证：AF=DC；

    （2）若AD=CF，试判断四边形AFDC是什么样的四边形？并证明你的结论．

    见解析；矩形. 【解析】试题分析：因为AF∥DC，E为AD的中点，即可根据AAS证明△AEF≌△DEC，故有AF=DC；由（1）知，AF=DC且AF∥DC，可得四边形AFDC是平行四边形，又因为AD=CF，故可根据对角线相等的平行四边形是矩形进行判定． 试题解析：（1）∵AF∥DC， ∴∠AFE=∠DCE， 又∵∠AEF=∠DEC（对顶角相等），AE=DE（E为AD的中点）， ∴...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年内蒙古中考数学二模试卷 题型：填空题

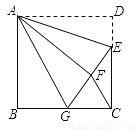
    如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论是________．

    ①②③④⑤ 【解析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE=∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+...

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型：解答题

    如图以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点F.

    （1）求证：DF⊥AC；

    （2）若∠ABC=30°，求tan∠BCO的值.

    (1)证明见解析; (2) tan∠BCO=. 【解析】试题分析：（1）连接OD，根据三角形的中位线定理可求出OD∥AC，根据切线的性质可证明DE⊥OD，进而得证． （2）过O作OF⊥BD，根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长，根据三角函数的定义求解． 试题解析：证明:连接OD ∵DE为⊙O的切线, ∴OD⊥DE ∵O为AB中点, D为BC的中点...

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型：填空题

    若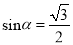，则锐角____

    60° 【解析】根据特殊角30°，45°，60°的三角函数值，可知α的值为60°. 故答案为：60°.

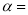    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型：单选题

    在比例尺为1：38 000的城市交通地图上，某条道路的长为5 cm，则它的实际长度为( )

    A. 0.19 km B. 1.9 km C. 19 km D. 190 km

    B 【解析】设这条道路的实际长度为xcm，则可得1:38000=5：x，解得x=190000=1.9km. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：填空题

    如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，

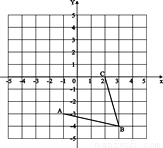
    （1）写出点D的坐标_____________；

    （2）线段BC的长为____________；

    （3）菱形ABCD的面积为____________．

    （1）D（－2，1） （2） （3）15 【解析】(1)菱形ABCD如图所示,D(?2,1)； (2)由勾股定理得,BC==； (3)S菱形ABCD=2S△ABC,=2(4×4?×3×3?×1×4?×1×4)=2(16?4.5?2?2)=2×7.5=15， 故答案为：(1)(?2，1)；(2) ；(3)15.

    查看答案和解析>>

    科目：初中数学 来源：四川省数学八年级下册期末复习测试卷 题型：单选题

    如图所示，有一张一个角为60°的直角三角形纸片，沿其一条中位线剪开后，不能拼成的四边形是( )

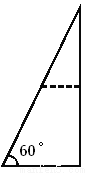
    A. 邻边不等的矩形 B. 等腰梯形

    C. 有一角是锐角的菱形 D. 正方形

    D 【解析】试题分析：如图：此三角形可拼成如图三种形状， （1）为矩形，∵有一个角为60°，则另一个角为30°，∴此矩形为邻边不等的矩形； （2）为菱形，有两个角为60°； （3）为等腰梯形． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省佛山市中考数学模拟试卷（3） 题型：解答题

    已知二次函数y=x2+2x﹣3，

    （1）用描点法画出y=x2+2x﹣3的图象．

    （2）根据你所画的图象回答问题：当x　 　时，函数值y随x的增大而增大，当x　 　时，函数值y随x的增大而减小．

    【解析】
    列表得：

    X

    Y

    描点、连线

    （1）详见解析；（2）x＞﹣1，x＜﹣1． 【解析】试题分析： （1）由解析式可知抛物线的对称轴为直线，因此可取-4、-3、-2、-1、0、1、2计算出对应的y的值进行列表，然后在坐标系中描出对应的点，并用平滑的曲线将这些点连起来，即可得到所求抛物线； （2）根据图象回答所求问题即可. 试题解析： （1）列表如下： X ﹣4 ﹣3 ﹣2 ...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型：单选题

    下列运算正确的是（　　）

    A. 3x﹣2x=1 B. ﹣2x﹣2=﹣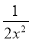 C. （﹣a）2•a3=a6  D. （﹣a2）3=﹣a6

    D 【解析】A. 3x﹣2x=x，故A选项错误；B. ﹣2x﹣2=﹣ ，故B选项错误；C. （﹣a）2•a3=a5，故C选项错误；D. （﹣a2）3=﹣a6，故D选项正确， 故选D.

    查看答案和解析>>

    同步练习册答案