
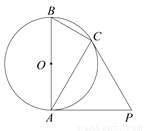
如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,点C,若∠P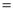 60°,PA
60°,PA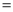
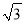 ,则AB的长为__________.
,则AB的长为__________.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源:北京市丰台区2017-2018学年七年级上学期期末考试数学试卷(WORD版) 题型:解答题
已知:线段AB = 2,点D是线段AB的中点,延长线段AB到C,BC = 2AD.求线段DC的长.

查看答案和解析>>
科目:初中数学 来源:内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
平方等于64的数为________
【解析】试题分析:因为82=64,(-8)2=64, 所以平方等于64的数是±8. 故答案为±8.查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
已知二次函数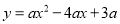 .
.
(1)该二次函数图象的对称轴是x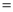 ;
;
(2)若该二次函数的图象开口向下,当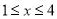 时,
时, 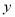 的最大值是2,求当
的最大值是2,求当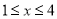 时,
时, 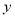 的最小值;
的最小值;
(3)若对于该抛物线上的两点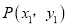 ,
, 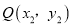 ,当
,当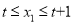 ,
, 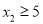 时,均满足
时,均满足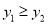 ,请结合图象,直接写出
,请结合图象,直接写出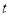 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
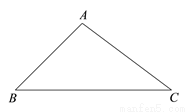
如图,在△ABC中,∠B为锐角, AB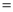
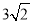 ,AC
,AC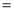 5,
5, 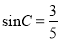 ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:填空题
方程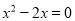 的根为__________.
的根为__________.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:单选题
在△ABC中,∠C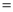 90°.若AB
90°.若AB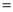 3,BC
3,BC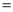 1,则
1,则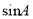 的值为( )
的值为( )
A. 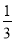 B.
B. 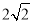 C.
C. 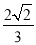 D.
D. 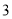
查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:填空题
若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为__________.
6 【解析】设这个扇形的半径为,根据题意可得: ,解得: . 故答案为: .查看答案和解析>>
科目:初中数学 来源:云南省2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
计算:
(1)(﹣a2)3•4a (2)2x(x+1)+(x+1)2.
(1)-4a7; (2) 3x2+4x+1. 【解析】试题分析:(1)根据幂的乘方、同底数幂的乘法进行计算即可; (2)根据单项式乘以多项式以及完全平方公式进行计算即可. 【解析】 (1)原式=﹣a6•4a =﹣4a7; (2)原式=2x2+2x+x2+2x+1 =3x2+4x+1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com