练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某种商品因换季准备打折出售，如果按原定价的七五折出售，将赔25元，而按原定价的九折出售，将赚20元，则这种商品的原价是(　　)

    A. 500元 B. 400元 C. 300元 D. 200元

    C 【解析】【解析】 设这种商品的原价是x元，根据题意得：75%x+25=90%x﹣20，解得x=300．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：单选题

    下列命题是假命题的是（ ）

    A. 三角形的角平分线都在三角形内部 B. 三角形的三条高都在三角形内部

    C. 三角形的三条中线都在三角形内部 D. 三角形的三条角平分线相交于一点

    B 【解析】A. ∵ 三角形的角平分线都在三角形内部是真命题，故不符合题意； B. ∵钝角三角形有两条条高在三角形外部，∴三角形的三条高都在三角形内部是假命题，故符合题意； C. ∵三角形的三条中线都在三角形内部是真命题，故不符合题意； D. ∵三角形的三条角平分线相交于一点是真命题，故不符合题意； 故选B.

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，矩形OABC的面积为24，它的对角线OB与双曲线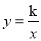相交于点D，且D为OB的中点，则k的值为（ ）

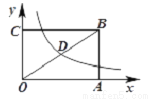
    A. 3 B. 6 C. 9 D. 12

    B 【解析】根据反比例函数解析式可得D点的坐标为（），然后根据中点的性质，可得B点的坐标为：（），然后可根据矩形的面积可求得2x×=24，解得k=6. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：填空题

    一艘轮船航行于A，B两个码头之间，顺水航行需3小时，逆水航行需5小时．已知水流速度为4千米/时，则两码头之间的距离为________千米．

    60 【解析】【解析】 设船在静水中的速度为x千米/时，则顺水速度为（x+4）千米/时，逆水航行速度为（x﹣4）千米/时，由题意得 3（x+4）=5（x﹣4），解得：x=16，∴两码头间的距离为：3×（16+4）=60（千米）． 故答案为：60．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：单选题

    下列说法错误的是(　　)

    A. 若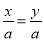，则x＝y B. 若x2＝y2，则－4ax2＝－4ay2

    C. 若a＝b，则a－3＝b－3 D. 若ac＝bc，则a＝b

    D 【解析】解：A．若，等式两边同时乘以a，可得x=y，正确； B．若x2=y2，等式两边同时乘以﹣4a，可得﹣4ax2=﹣4ay2，正确； C．若a=b，等式两边同时减去﹣3，可得a﹣3=b﹣3，正确； D．若ac=bc，则a不一定等于c，例如3×0=4×0，但是3≠4，故错误； 故选D．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

    综合与实践

    问题情境

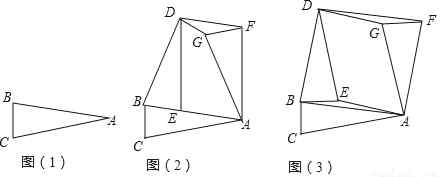
    在综合实践课上，老师让同学们“以三角形的旋转”为主题进行数学活动，如图（1），在三角形纸片ABC中，AB=AC，∠B=∠C=α．

    操作发现

    （1）创新小组将图（1）中的△ABC以点B为旋转中心，逆时针旋转角度α，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转角度α，得到△AFG，连接DF，得到图（2），则四边形AFDE的形状是　 　．

    （2）实践小组将图（1）中的△ABC以点B为旋转中心，逆时针逆转90°，得到△DBE，再将△ABC以点A为旋转中心，顺时针旋转90°，得到△AFG，连接DF、DG、AE，得到图（3），发现四边形AFDB为正方形，请你证明这个结论．

    拓展探索

    （3）请你在实践小组操作的基础上，再写出图（3）中的一个特殊四边形，并证明你的结论．

    （1）平行四边形；（2）证明见解析（3）四边形AEDG是平行四边形． 【解析】试题分析：（1）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形； （2）由旋转的性质和旋转角度可求得DE∥AF，且DE＝AF，可证明四边形AFDE为平行四边形，再由旋转角是90°，即可得出结论； （3）由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论． ...

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：填空题

    如图，在四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥CD，垂足为E，若线段AE=10，则S四边形ABCD=_____．

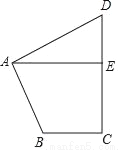
    100 【解析】试题分析：过A作AF⊥BC，交CB的延长线于F， ∵AE⊥CD，∠C＝90° ∴∠AED＝∠F＝∠C＝90°，∴四边形AFCE是矩形， ∴∠FAE＝90°， ∵∠DAB＝90°， ∴∠DAE＝∠BAF＝90°﹣∠BAE， 在△AFB和△AED中， ， ∴△AFB≌△AED（AAS）， ∴AE＝AF＝10，S△AFB＝S△A...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：解答题

    如图，湖心岛上有一凉亭，现欲利用湖岸边的开阔平整地带，测量凉亭顶端到湖面所在平面的高度AB（见示意图），可供使用的工具有测倾器、皮尺．

    （1）请你根据现有条件，设计一个测量凉亭顶端到湖面所在平面的高度AB的方案，画出测量方案的平面示意图，并将测量的数据标注在图形上（所测的距离用m，n，…表示，角用α，β，…表示，测倾器高度忽略不计）；

    （2）根据你所测量的数据，计算凉亭到湖面的高度AB（用字母表示）．

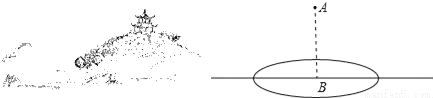
    （1）见解析；（2）x=． 【解析】试题分析：（1）可在距离AB的地方用测倾器测2次，并量出两个测试点之间的距离； （2）设AB为未知数，可用不同的方式表示出BD长，列出方程求解即可． 试题解析：（1）如图所示，在点C测得∠ACB=α，在点D测得∠ADB=β，测得DC=m． （2）在Rt△ABC中，设AB=x，BC=x÷tanα， 在Rt△ABD中，BD=x÷tanβ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    下列各直线的表示法中，正确的是(　　)

    A. 直线ab B. 直线Ab C. 直线A D. 直线AB

    D 【解析】根据直线的两种表示法：用一个小写字母表示，或用两个大些字母（直线上的）表示，可得选项D正确，故选D.

    查看答案和解析>>

    同步练习册答案