练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有理数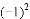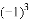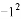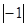，，，，-（-1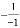），中，其中等于1的个数是（ ）

    A. 3个 4个 B. 5个 C. 6个

    B 【解析】试题分析：故等于1的有4个数．故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）练习 题型：解答题

    已知：如图，在△ABC中，∠ABC=90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D．

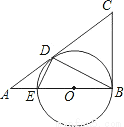
    （1）求证：BC=CD；

    （2）求证：∠ADE=∠ABD；

    （1）证明见解析；（2）证明见解析. 【解析】 试题分析：从切线的性质出发，通过切线与弦所夹的角与弧弦夹角相等，即得到∠CDB=∠CBA；由切线的性质而求得． 试题解析：（1）证明：∵∠ABC=90°， ∴OB⊥BC ∵OB是⊙O的半径， ∴CB为⊙O的切线． 又∵CD切⊙O于点D， ∴BC=CD； （2）证明：∵BE是⊙O的直径， ∴∠...

    查看答案和解析>>

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，在△ABC中，BC边上的垂直平分线DE与边BC交于点D，边AB交于点E．若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为（　　）

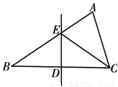
    A. 12 B. 6 C. 24 D. 36

    B 【解析】因为ED垂直平分BC，所以EB=EC，DB=DC. 因为△ABC与四边形AEDC的周长之差为12， 所以AE+EB+BD+DC+CA-(AE+ED+DC+CA)=12，即BE+BD-DE=12①. 因为CE+CD+DE=24，即BE+BD+DE=24②. ②-①得DE=6. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    解方程（1）5（x-1）-2（3x-1）=4x-1 （2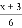）=1-

    （1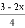）x=-0.4 ；（2）x=0.75. 【解析】试题分析：解一元一次方程，先去分母、括号，然后移项、合并同类项，最后把未知数的系数化为1即可. 试题解析：⑴ ， 去括号，得 ， 移项、合并同类项，得 未知数系数化1，得 . ⑵ ， 去分母，得 ， 去括号，得 ， 移项、合并同类项，得 未知数系数化1，得 .

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    下列说法正确的是（ ）

    (A)a是代数式，1不是代数式 (B)表示a、b、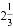 的积的代数式为 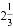ab

    (C)代数式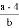 的意义是：a与4的差除b的商 (D) 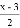是二项式，它的一次项系数是

    D 【解析】试题解析：A选项，1也是代数式，故错误；B选项，代数式应为 ，故错误；C选项，意义是 与4的差除以 的商，故错误；D选项， ，它的一次项系数为 ，故正确. 故本题应选D.

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：解答题

    某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1．9元收费．如果超过20吨，未超过的部分按每吨1．9元收费，超过的部分按每吨2．8元收费．设某户每月用水量为x吨，应收水费为y元．

    （1）分别写出每月用水量未超过20吨和超过20吨，y与x间的函数关系式；

    （2）若该城市某户5月份水费平均为每吨2．2元，求该户5月份用水多少吨？

    （1）当x≤20时，y＝1．9x、当x＞20时，y=2．8x－18；（2）30吨． 【解析】 试题分析：本题分x≤20和x＞20两种情况分别列出函数解析式；首先根据平均水费得出用水量的范围，然后代入函数解析式计算用水量． 试题解析：（1）当x≤20时，y＝1．9x； 当x＞20时，y＝1．9×20＋（x－20）×2．8＝2．8x－18 ． （2）因为5月份水费平均为每...

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：解答题

    已知正比例函数y1=k1x与一次函数y2=k2x-9的图象交于点P(3,-6)，求 这两个函数的关系式．

    y=-2x y=x-9 【解析】试题分析：将P（3，-6）分别代入正比例函数y1=k1x与一次函数y2=k2x-9的解析式即可得. 试题解析：∵y1=k1x过（3，-6），∴-6=3k1，解得k1=-2，∴y1=-2x， 又∵y2=k2x-9过（3，-6），∴-6=3k2-9，解得k2=1，∴y2=x-9.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）测试 题型：填空题

    如图，PA、PB分别切圆O于A、B两点，并与圆O的切线分别相交于C、D两点，已知PA=7cm，则△PCD的周长等于_________．

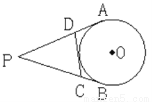
    14. 【解析】 试题分析：由于DA、DC、BC都是⊙O的切线，可根据切线长定理，将△PCD的周长转换为PA、PB的长，然后再进行求解． 试题解析：如图，设DC与⊙O的切点为E； ∵PA、PB分别是⊙O的切线，且切点为A、B； ∴PA=PB=7cm； 同理，可得：DE=DA，CE=CB； 则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=P...

    查看答案和解析>>

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：填空题

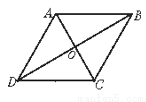
    如下左图，菱形ABCD中，AC、BD相交于O，若OD=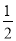AD，则四个内角为________.

    60°，120°，60°，120° 【解析】因为四边形ABCD是菱形,所以AC⊥BD, ∠ADB=∠CDO=∠ABD=∠CBD, 因为OA=AD, 所以∠ADO=30°, 所以∠ADC=∠ABC=60°, ∠DAB=∠DCB=120°. 故答案为: 60°, 120°, 60°, 120°.

    查看答案和解析>>

    同步练习册答案