练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知正比例函数y1=k1x与一次函数y2=k2x-9的图象交于点P(3,-6)，求 这两个函数的关系式．

    y=-2x y=x-9 【解析】试题分析：将P（3，-6）分别代入正比例函数y1=k1x与一次函数y2=k2x-9的解析式即可得. 试题解析：∵y1=k1x过（3，-6），∴-6=3k1，解得k1=-2，∴y1=-2x， 又∵y2=k2x-9过（3，-6），∴-6=3k2-9，解得k2=1，∴y2=x-9.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型：解答题

    如图，AB = DE，AC = DF，BE = CF. 求证：AB∥DE.

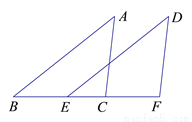
    见解析 【解析】试题分析: 求出BC=EF，根据SSS证△ABC≌△DEF，推出∠B=∠DEF，根据平行线判定推出即可． 试题解析: ∵BE＝CF， ∴BC=EF ， 在△ABC与△DEF中， ∴△ABC≌△DEF ， ∴∠B=∠DEF ， ∴AB∥DE.

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    甲乙两地相距200km，快车速度为120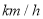 ，慢车速度为80 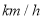，慢车从甲地出发，快车从乙地出发，

    （1）如果两车同时出发，相向而行，出发后几时两车相遇？相遇时离甲地多远？

    （2）如果两车同时出发，同向（从乙开始向甲方向）而行，出发后几时两车相遇?

    （1）1小时，80km；（2）5小时. 【解析】试题分析： (1)相遇问题，设 小时后两车相遇，则两车行驶距离之和为甲乙两地距离； (2)追及问题，设小时后两车相遇，则两车行驶距离之差为甲乙两地距离； 试题解析：(1)设小时后两车相遇，则 由题意， ， 解之，得 ， 故1小时后两车相遇，相遇时离甲地80 km . (2)设 小时后两车相遇，则 ...

    查看答案和解析>>

    科目：初中数学 来源：安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    有理数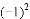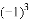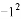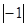，，，，-（-1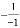），中，其中等于1的个数是（ ）

    A. 3个 4个 B. 5个 C. 6个

    B 【解析】试题分析：故等于1的有4个数．故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：解答题

    地表以下岩层的温度t (℃)，随着所处的深度 h (km)的变化而变化，t与h 在一定范围内近似成一次函数关系．

    (1)根据下表，求 t(℃)与h (km)之间的函数关系式.

    (2)求当岩层温度达到 1770 ℃时，岩层所处的深度为多少千米？

    (1) t＝35h＋20；(2)岩层温度达到 1770 ℃ 【解析】试题分析：（1）任取两对数，用待定系数法求函数解析式．用其余的数对验证即可； （2）知道温度求深度，就是知道函数值求自变量的值，将相应数值代入（1）中解析式即可得． 试题解析：（1）设 t 与 h 之间的函数关系式为 t＝kh＋b， 取表格中的两对对应值 h＝0，t＝20；h＝2，t＝90， 代入得 ...

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：填空题

    点（-3，2），（a，a+1）在函数y=kx-1的图象上，则k= ，a= ．

    -1．-1． 【解析】 试题解析：把（-3，2）代入y=kx-1，得-3k-1=2．∴k=-1． ∴解析式为：y=-x-1， 把（a，a+1）代入y=-x-1，得：-a-1=a+1， 解得a=-1．

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：单选题

    一次函数y=kx+b（k≠0）的图象如图所示，当y＞0时，x的取值范围是（ ）

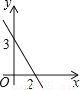
    A. x＜0 B. x＞0 C. x＜2 D. x＞2

    C 【解析】试题分析：因为直线y=kx+b与x轴的交点坐标为（2，0）， 由函数的图象可知当y＞0时，x的取值范围是x＜2． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：单选题

    Rt△ABC中，∠C=90°，AB=10，AC=6，以C为圆心作⊙C和AB相切，则⊙C的半径长为（）

    A. 8 B. 4 C. 9．6 D. 4．8

    D 【解析】作CD⊥AB于D,如图所示, 因为∠C=90°,AB=10,AC=6, 所以BC=8, 因为AC·BC=AB·CD, CD=, 因为⊙C与AB相切, 所以CD为⊙C的半径, 即的半径长为,故选D.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 25.2用列举法求概率测试 题型：填空题

    在平面直角坐标系中，作△OAB，其中三个顶点分别是O（0，0），B（1，1），A（x，y）（-2≤x≤2，-2≤y≤2，x，y均为整数），则所作△OAB为直角三角形的概率是______．

    ． 【解析】 试题解析：∵A（x，y）（-2≤x≤2，-2≤y≤2，x，y均为整数）， ∴A点坐标可以为： （-2，-1），（-2，0），（-2，1），（-2，2）， （-1，-2），（-1，0），（-1，1），（-1，2）， （0，-2），（0，-1），（0，1），（0，2）， （1，-2），（1，-1），（1，0），（1，2）， （2，-2），（...

    查看答案和解析>>

    同步练习册答案