练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在直角坐标平面内，直线y=x+2分别与x轴、y轴交于点A、C．抛物线y=﹣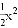+bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．

    （1）求上述抛物线的表达式；

    （2）联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；

    （3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．

    （1）y=﹣x+2；（2）；（3）（﹣，）或（﹣3，2）． 【解析】试题分析：（1）由直线得到A、C的坐标，然后代入二次函数解析式，利用待定系数法即可得； （2）过点E作EH⊥AB于点H，由已知可得 ，从而可得、的长，然后再根据三角函数的定义即可得； （3）分情况讨论即可得. 试题分析：（1）由已知得A(-4，0)，C(0，2) ， 把A、C两点的坐标代入得， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

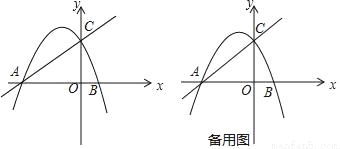
    如图，已知C是AB的中点，D是AC的中点，E是BC的中点．

    （1）若AB=16cm，求DE的长；

    （2）若CE=4cm，求DB的长．

    （1）8cm；（2）12cm． 【解析】试题分析：（1）根据中点的概念，分别求出AC，BC，DC，CE的长，最后由DE=DC+CE求得DE的长； （2）由(1)知AD=DC=CE=BE，从而得到CE=BD，即可得到结论． 试题解析：(1)∵C是AB的中点，∴AC=BC=AB=8(cm)． ∵D是AC的中点，∴AD=DC=AC=4(cm)． ∵E是BC的中点，∴CE=B...

    查看答案和解析>>

    科目：初中数学 来源：云南省2018届九年级上学期期中考试数学试卷 题型：填空题

    点P（2，-1）关于原点成中心对称的点Q的坐标是_____________.

    (-2,1) 【解析】试题解析：根据中心对称的性质，得点P（2，-1）关于中心对称的点的坐标为（-2，1）． 故答案为：（-2，1）．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县七年级（上）期末数学试卷（五四学制） 题型：填空题

    计算：|﹣5|=_____．

    5 【解析】【解析】 |﹣5|=5．故答案为：5．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县七年级（上）期末数学试卷（五四学制） 题型：单选题

    下列各式的计算，结果正确的是（　　）

    A. 3a+2b=5ab B. m2﹣n2=0 C. 5x+2x=7x2 D. 5xy﹣5yx=0

    D 【解析】解：A．不是同类项不能合并，故A错误； B．不是同类项不能合并，故B错误； C．系数相加字母及指数不变，故C错误； D．系数相加字母及指数不变，故D正确； 故选D．

    查看答案和解析>>

    科目：初中数学 来源：上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    计算： ．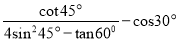

    【解析】试题分析：将各特殊角的三角形函数值代入进行计算即可. 试题解析：原式= = = =.

    查看答案和解析>>

    科目：初中数学 来源：上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    已知线段AB=4，点P是线段AB的黄金分割点，且AP＜BP，那么AP的长为_____．

    （6﹣2）cm． 【解析】由题意得：BP2=AP·AB，BP=AB-AP， 即：（4-AP）2=4AP， 解得：AP= ， 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型：解答题

    如图，在四边形 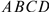中，，．请你添加一条线把它分成两个全等三角形，并给出证明．

    见解析 【解析】试题分析：连接AC，根据全等三角形的判定解答即可． 试题解析：【解析】 连接AC，则△ABC≌△ADC，证明如下： 在△ABC与△ADC中，∵AB=AD，AC=AC，CB=CD，∴△ABC≌△ADC．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（人教版）：期中检测题 题型：单选题

    如图，任意四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，对于四边形EFGH的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）

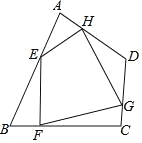
    A．当E，F，G，H是各边中点，且AC=BD时，四边形EFGH为菱形

    B．当E，F，G，H是各边中点，且AC⊥BD时，四边形EFGH为矩形

    C．当E，F，G，H不是各边中点时，四边形EFGH可以为平行四边形

    D．当E，F，G，H不是各边中点时，四边形EFGH不可能为菱形

    D 【解析】 试题分析： 根据题意，可知，连接四边形各边中点所得的四边形必为平行四边形，根据中点四边形的性质进行判断： A．当E，F，G，H是各边中点，且AC=BD时，EF=FG=GH=HE，故四边形EFGH为菱形，故A正确； B．当E，F，G，H是各边中点，且AC⊥BD时，∠EFG=∠FGH=∠GHE=90°，故四边形EFGH为矩形，故B正确； C．当E，F，...

    查看答案和解析>>

    同步练习册答案