
不等式组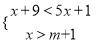 的解集是x>2,则m的取值范围是____.
的解集是x>2,则m的取值范围是____.
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
在一幅长80cm,宽50cm的矩形风景画的四周镶等宽的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2,设金色纸边的宽为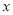 cm,根据题意所列方程正确的是( )
cm,根据题意所列方程正确的是( )
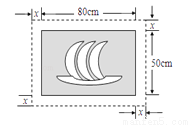
A. 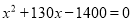 B.
B. 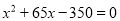
C. 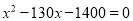 D.
D. 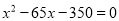
查看答案和解析>>
科目:初中数学 来源:江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型:解答题
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)
(2)任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。
(1) ;(2)见解析 【解析】试题分析:(1)直接利用概率公式求解; (2)画树状图展示所有12种等可能性结果数,再找出满足条件的结果数,然后根据概率公式求解. 试题解析:解:(1)∵共有乙、丙、丁三位同学,恰好选中乙同学的只有一种情况,∴P(恰好选中乙同学)=; (2)画树状图得: ∵所有出现的等可能性结果共有12种,其中满足条件的结果有2种. ∴P(恰好选...查看答案和解析>>
科目:初中数学 来源:江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型:单选题
已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )
A. 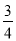 或1 B.
或1 B. 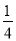 或1 C.
或1 C. 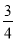 或
或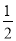 D.
D. 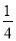 或
或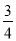
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
已知,a、b、c为△ABC的三边长,b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求△ABC的周长,并判断△ABC的形状.
△ABC的周长为:2+2+3=7,△ABC是等腰三角形. 【解析】试题分析: 根据已知条件可求得a、b、c的值,其中a的值有两个,再由三角形三边间的关系进行检验,看是否都能围成三角形,最后再求周长和判定三角形的形状; 试题解析: 【解析】 ∵(b﹣2)2+|c﹣3|=0, ∴ b﹣2=0,c﹣3=0, 解得:b=2,c=3, ∵ a为方程|a﹣4|=2的...查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
算术平方根和立方根都等于本身的数有_________.
1,0 【解析】1的算术平方根是1,立方根是1,0的算术平方根和立方根都是0,所以算术平方根和立方根都等于本身的数有0和1.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
至少有两边相等的三角形是( )
A. 等边三角形 B. 等腰三角形 C. 等腰直角三角形 D. 锐角三角形
B 【解析】①两边相等的三角形称为等腰三角形,该等腰三角形可以是等腰直角三角形,也有可能是锐角三角形,也有可能是钝角三角形; ②当有三边相等时,该三角形是等边三角形,等边三角形是一特殊的等腰三角形, 故选B.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=________cm.
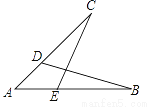
查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年八年级上学期期末模拟数学试卷 题型:单选题
如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
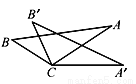
A. 1 B. 2
C. 3 D. 4
B 【解析】试题解析:当①②③为条件,④为结论时: ∵∠A′CA=∠B′CB, ∴∠A′CB′=∠ACB, ∵BC=B′C,AC=A′C, ∴△A′CB′≌△ACB, ∴AB=A′B′, 当①②④为条件,③为结论时: ∵BC=B′C,AC=A′C,AB=A′B′, ∴△A′CB′≌△ACB, ∴∠A′CB′=∠ACB, ∴∠A′CA=∠B′CB. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com