练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，EF过矩形ABCD对角线的交点O，且分别交AD、BC于点E、F已知AB=3，BC=4，则图中阴影部分的面积是（　　）

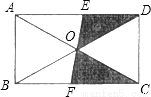
    A. 3 B. 4 C. 6 D. 12

    A 【解析】∵四边形ABCD是矩形，∴OB=OD，AD∥BC，∴∠CBD=∠ADB. ∵∠BOF=∠DOE，∴△BOF≌△DOE，∴S△DOE=S△BOF. ∴阴影部分的面积为S△BOF+S△COF=S△OBC=S矩形ABCD=×4×3=3. 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：填空题

    一次函数y=x+4的图象经过点P(a，b)和Q(c，d)，则b(c－d)－a(c－d)的值为_______

    -16 【解析】【解析】 ∵一次函数y=x+4的图象经过P（a，b）和Q（c，d），∴a+4=b，c+4=d，即b﹣a=4，c﹣d=﹣4，∴原式=（c﹣d）（b﹣a）=（﹣4）×4=－16．故答案为：－16．

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

    如图所示，点E为正方形ABCD内部的一点，且△ABE为等边三角形，试求∠ADE的度数．

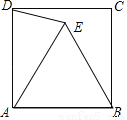
    75° 【解析】试题分析： 先证AD=AE=AB，由△ABE是等边三角形可得∠DAE，在等腰△ADE中，可求∠ADE. 试题解析： 【解析】 ∵E为正方形ABCD内一点，且△ABE是等边三角形， ∴∠DAB=90°，∠EAB=60°，AD=AE=BE， ∴∠DAE=∠DAB﹣∠EAB=30°， ∴∠ADE=∠AED==75°．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：解答题

    如图，在矩形ABCD中，连接对角线AC，BD，延长BC至点E，使BC=CE，连接DE．

    求证：DE=AC．

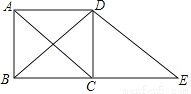
    证明见解析 【解析】试题分析： 证明CD是线段BE的垂直平分线，得到DB=DE，又因为DB=AC，则得证. 试题解析： ∵四边形ABCD是矩形，∴AC=BD，∠BCD=90°， ∵BC=CE，∴DC是BE的中垂线，∴BD=DE， ∴DE=AC．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：填空题

    如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E．若DE=DC=1，AE=2EM，则BM的长为__．

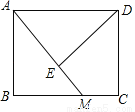
    【解析】试题解析：∵四边形ABCD是矩形， ∴∠AMB=∠DAE， ∵DE=DC， ∴AB=DE， ∵DE⊥AM， 在△ABM和△DEA中, ∴AM=AD， ∵AE=2EM， ∴BC=AD=3EM， 连接DM，如图所示： 在和中, ∴EM=CM， ∴BC=3CM， 设EM=CM=x，则BM=2x，AM=BC=3x， ...

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：解答题

    某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品，根据市场调研，发现如下两种信息：

    信息一：销售甲款护肤品所获利润y（元）与销售量x（件）之间存在二次函数关系y=ax2+bx．在x=10时，y=140；当x=30时，y=360．

    信息二：销售乙款护肤品所获利润y（元）与销售量x（件）之间存在正比例函数关系y=3x．请根据以上信息，解答下列问题；

    （1）求信息一中二次函数的表达式；

    （2）该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件，请设计一个营销方案，使销售甲、乙两款护肤品获得的利润之和最大，并求出最大利润．

    （1）y=-0.1x2+15x；（2）购进甲产品60件，购进乙产品40件，最大利润是660元 【解析】试题分析：（1）把两组数据代入二次函数解析式，然后利用待定系数法求解即可； （2）设购进甲产品m件，则购进乙产品（10-m）件，销售甲、乙两种产品获得的利润之和为W元，根据总利润等于两种产品的利润的和，列式整理得到W与m的函数关系式，再根据二次函数的最值问题解答． 试题解析：【解...

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：填空题

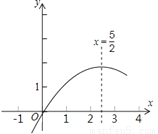
    如图，二次函数y=ax2+bx+c（a≠0）的图象过原点O，且该图象的对称轴是直线x=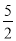，若函数值y＞0．则x取值范围是_________．

    0＜x＜5 【解析】【解析】 ∵抛物线图象过原点O，且该图象的对称轴是直线x=，∴抛物线与x轴的另一个交点的坐标为（5，0），∴若函数值y＞0，则x取值范围是0＜x＜5．故答案为：0＜x＜5．

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：单选题

    过钝角三角形的三个顶点所作圆的圆心在（）

    A． 三角形上 B． 三角形外 C． 三角形内 D． 以上皆有可能

    B. 【解析】 试题分析：根据过三角形的三个顶点的圆是三角形外接圆，再利用锐角三角形、直角三角形、钝角三角形外心位置不同得出答案．解答：【解析】 过三角形的三个顶点的圆是三角形外接圆， 当过锐角三角形三个顶点，圆心在三角形内部； 当过直角三角形三个顶点，圆心在三角形斜边上； 当过钝角三角形三个顶点，圆心在三角形外部； 故选B． 考点:三角形的外接圆与外心...

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第1讲 实数概念与运算 题型：单选题

    如果向北走6步记作＋6步，那么向南走8步记作(　　)

    A. ＋8步 B. －8步

    C. ＋14步 D. －2步

    B 【解析】试题分析：“正”和“负”是表示互为相反意义的量，向北走记作正数，那么向北的反方向，向南走应记为负数． 【解析】 ∵向北走6步记作+6步， ∴向南走8步记作?8步， 故选A.

    查看答案和解析>>

    同步练习册答案