
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
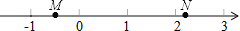
A. m+n<0 B.  m<
m< n C. |m|
n C. |m| |n|>0 D. 2+m<2+n
|n|>0 D. 2+m<2+n
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:填空题
已知点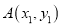 ,
, 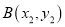 在二次函数
在二次函数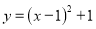 的图象上,若
的图象上,若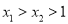 ,则
,则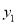 __________
__________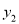 .(填“
.(填“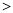 ”“
”“ 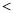 ”“
”“ 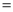 ”)
”)
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:解答题
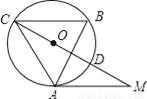
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为( )
A. -2 B. 2 C. 4 D. -3
A 【解析】试题分析:根据一元二次方程根与系数的关系,利用两根和,两根积,即可求出a的值和另一根. 设一元二次方程的另一根为x1,则根据一元二次方程根与系数的关系, 得﹣1+x1=﹣3, 解得:x1=﹣2.查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:解答题
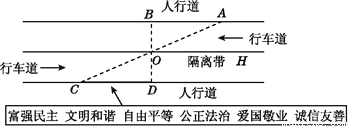
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
下列各数:1.414,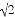 ,-
,- ,0,其中是无理数的是( )
,0,其中是无理数的是( )
A. 1.414 B. 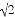 C. -
C. - D. 0
D. 0
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
如果“盈利5%”记作+5%,那么-3%表示( )
A. 亏损3% B. 亏损8% C. 盈利2% D. 少赚3%
A 【解析】试题分析:已知盈利5%”记作+5%,根据正负数的意义可得﹣3%表示表示亏损3%.故答案选A.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:单选题
设函数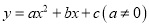 ,其图象都经过点
,其图象都经过点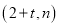 和点
和点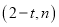 ,且图像又经过点
,且图像又经过点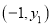 、
、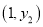 、
、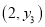 、
、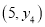 则函数值
则函数值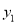 、
、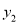 、
、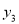 、
、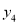 中,最小的一个不可能是( )
中,最小的一个不可能是( )
A. 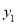 B.
B. 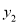 C.
C. 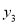 D.
D. 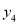
查看答案和解析>>
科目:初中数学 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:填空题
若二次函数y=x2+2x+m的图象与x轴没有公共点,则m的取值范围是________.
m>1 【解析】∵二次函数y=x2+2x+m的图象与x轴没有公共点, ∴方程x2+2x+m=0没有实数根, ∴判别式△=22?4×1×m<0, 解得:m>1; 故答案为:m>1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com