
如果“盈利5%”记作+5%,那么-3%表示( )
A. 亏损3% B. 亏损8% C. 盈利2% D. 少赚3%
A 【解析】试题分析:已知盈利5%”记作+5%,根据正负数的意义可得﹣3%表示表示亏损3%.故答案选A. 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图, 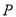 是等边三角形
是等边三角形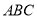 内的一点,连结
内的一点,连结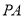 、
、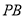 、
、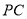 ,以
,以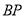 为边作
为边作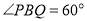 且
且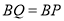 .连结
.连结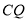 .
.
(1)观察并猜想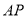 与
与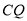 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若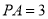 ,
, 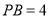 ,
, 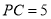 ,连结
,连结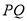 ,试判断
,试判断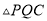 的形状,并说明理由.
的形状,并说明理由.
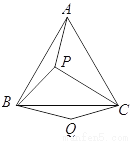
(3)在(2)的条件下,求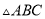 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
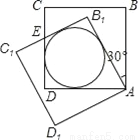
将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=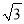 ,则四边形AB1ED的内切圆半径为( )
,则四边形AB1ED的内切圆半径为( )
A. 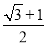 B.
B. 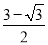 C.
C. 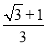 D.
D. 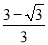
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
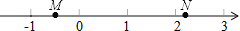
A. m+n<0 B.  m<
m< n C. |m|
n C. |m| |n|>0 D. 2+m<2+n
|n|>0 D. 2+m<2+n
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
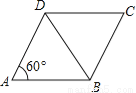
A. 1 B. 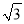 C. 2 D.
C. 2 D. 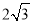
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:解答题
在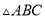 中,
中, 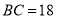 ,
, 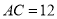 ,
, 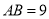 ,
,  ,
, 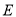 是直线
是直线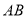 ,
, 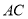 上的点,
上的点, 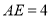 .若由
.若由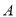 ,
, 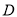 ,
, 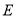 构成的三角形与
构成的三角形与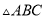 相似,求
相似,求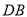 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:填空题
如图,在⊙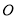 中,
中, 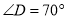 ,
, 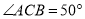 ,则
,则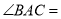 __________.
__________.

查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,在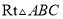 中,
中, 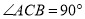 .
.
(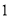 )用尺规在边
)用尺规在边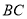 上求作一点
上求作一点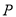 ,使
,使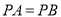 (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(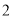 )连结
)连结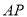 ,若
,若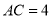 ,
, 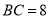 ,试求
,试求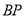 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.

(1)如果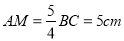 ,求MN的长;
,求MN的长;
(2)若AC = xcm,BC = (10﹣x)cm,求MN的长.
(1)MN = 7cm;(2)MN = 5cm 【解析】试题分析:(1)根据M是线段AC的中点,AM=BC=5cm,于是得到AM=CM=5cm,BC=4cm,由于N是线段BC的中点,得到CN=BC=2cm,根据线段的和差即可得到结论; (2)根据M是线段AC的中点,N是线段BC的中点,于是得到CM=AC=xcm,CN=BC=(10﹣x)=5﹣x,根据MN=CN+CM即可得到结论. ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com